摘要:10. 设椭圆E: 过M(2.) .N(,1)两点.O为坐标原点. (I)求椭圆E的方程, (II)是否存在圆心在原点的圆.使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且?若存在.写出该圆的方程.并求|AB |的取值范围.若不存在说明理由. 解:(1)因为椭圆E: 过M(2.) .N(,1)两点, 所以解得所以椭圆E的方程为 (2)假设存在圆心在原点的圆.使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且,设该圆的切线方程为解方程组得,即, 则△=,即 ,要使,需使,即,所以,所以又,所以,所以,即或,因为直线为圆心在原点的圆的一条切线,所以圆的半径为,,,所求的圆为,此时圆的切线都满足或,而当切线的斜率不存在时切线为与椭圆的两个交点为或满足,综上, 存在圆心在原点的圆.使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且. 因为, 所以, , ①当时 因为所以, 所以, 所以当且仅当时取 = . ② 当时,. ③ 当AB的斜率不存在时, 两个交点为或,所以此时, 综上, |AB |的取值范围为即: [命题立意]:本题属于探究是否存在的问题,主要考查了椭圆的标准方程的确定,直线与椭圆的位置关系直线与圆的位置关系和待定系数法求方程的方法,能够运用解方程组法研究有关参数问题以及方程的根与系数关系.
网址:http://m.1010jiajiao.com/timu_id_4012099[举报]
(2012年高考四川卷理科22) (本小题满分14分)
已知![]() 为正实数,
为正实数,![]() 为自然数,抛物线
为自然数,抛物线![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,设
,设![]() 为该抛物线在点
为该抛物线在点![]() 处的切线在
处的切线在![]() 轴上的截距。
轴上的截距。
(Ⅰ)用![]() 和
和![]() 表示
表示![]() ;
;
(Ⅱ)求对所有![]() 都有
都有![]() 成立的
成立的![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
(本小题有两个小题供选做,考生只能在①、②题中选做一题!多做不给分)
①PT切⊙O于点T,PAB、PCD是割线,AB=35cm,CD=50cm,AC:DB=1:2,则PT=
②已知A(ρ1,θ1),B(ρ2,θ2)则AB=
.
..
查看习题详情和答案>>
①PT切⊙O于点T,PAB、PCD是割线,AB=35cm,CD=50cm,AC:DB=1:2,则PT=
60 cm
60 cm
②已知A(ρ1,θ1),B(ρ2,θ2)则AB=
|
|
(2009•崇明县二模)设椭圆C:
+
=1(a>b>0)的一个顶点坐标为A(0,-
),且其右焦点到直线y-x-2
=0的距离为3.
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
,0),求证点M的所有“相关弦”的中点在同一条直线上;
(3)根据解决问题(2)的经验与体会,请运用类比、推广等思想方法,提出一个与“相关弦”有关的具有研究价值的结论,并加以解决.(本小题将根据所提出问题的层次性给予不同的分值)
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
| 1 |
| 2 |
(3)根据解决问题(2)的经验与体会,请运用类比、推广等思想方法,提出一个与“相关弦”有关的具有研究价值的结论,并加以解决.(本小题将根据所提出问题的层次性给予不同的分值)
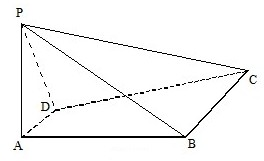 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2| 2 |
(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段GC上运动时,试提出一个研究有关四面P-BMN的问题(如体积、线面、面面关系等)并尝试解决.
(说明:本小题将根据你提出的问题的质量和解决难度分层评分;本小题的计算结果可以使用近似值,保留3位小数) 查看习题详情和答案>>
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2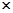 2列联表:
2列联表:
|
|
会围棋 |
不会围棋 |
总计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.
查看习题详情和答案>>

