摘要:设A.B分别是两个集合.为简明起见.设A.B分别是两个有限集 说明:这三个对应的共同特点是:对于左边集合A中 的任何一个元素.在右边集合B中都有唯一的元素和它对应 映射:设A.B是两个集合.如果按照某种对应法则f.对于集合 A中的任何一个元素.在集合B中都有唯一的元素和它对应. 这样的对应(包括集合A.B以及A到B的对应法则f)叫 做集合A到集合B的映射 记作: 象.原象:给定一个集合A到集合B的映射.且.如 果元素和元素对应.则元素叫做元素的象.元素叫 做元素的原象 关键字词:(学生思考.讨论.回答.教师整理.强调) ①“A到B :映射是有方向的.A到B的映射与B到A的映射往往不是同一个映射,A到B是求平方.B到A则是开平方.因此映射是有序的, ②“任一 :就是说对集合A中任何一个元素.集合B中都有元素和它对应.这是映射的存在性, ③“唯一 :对于集合A中的任何一个元素.集合B中都是唯一的元素和它对应.这是映射的唯一性, ④“在集合B中 :也就是说A中元素的象必在集合B中.这是映射的封闭性. 指出:根据定义.这三个对应都是集合A到集合B 的映射,注意到其中是多对一 思考:(1)为什么不是集合A到集合B的映射? 回答:对于(1).在集合A中的每一个元素.在集合B中都 有两个元素与之相对应.因此.(1)不是集合A到集 合B的映射 思考:如果从对应来说.什么样的对应才是一个映射? 一对一.多对一是映射 但一对多显然不是映射 辨析: ①任意性:映射中的两个集合A,B可以是数集.点集或由图形组成的集合等, ②有序性:映射是有方向的.A到B的映射与B到A的映射往往不是同一个映射, ③存在性:映射中集合A的每一个元素在集合B中都有它的象, ④唯一性:映射中集合A的任一元素在集合B中的象是唯一的, ⑤封闭性:映射中集合A的任一元素的象都必须是B中的元素.不要求B中的每一个元素都有原象.即A中元素的象集是B的子集. 映射三要素:集合A.B以及对应法则.缺一不可,
网址:http://m.1010jiajiao.com/timu_id_4010284[举报]
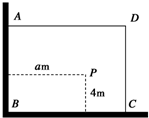 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )A、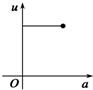 | B、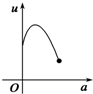 | C、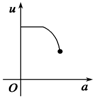 | D、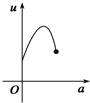 |
设两不同直线a,b的方向向量分别是
,
,平面α的法向量是
,
则下列推理①
⇒b∥α;②
⇒a∥b;③
⇒b∥α; ④
⇒b⊥α;
其中正确的命题序号是( )
| e1 |
| e2 |
| n |
则下列推理①
|
|
|
|
其中正确的命题序号是( )
查看习题详情和答案>>




