题目内容
设两不同直线a,b的方向向量分别是
,
,平面α的法向量是
,
则下列推理①
⇒b∥α;②
⇒a∥b;③
⇒b∥α; ④
⇒b⊥α;
其中正确的命题序号是( )
| e1 |
| e2 |
| n |
则下列推理①
|
|
|
|
其中正确的命题序号是( )
分析:根据两条直线的方向向量平行,则两条直线平行,两条直线的方向向量垂直,两条直线也垂直,直线的方向向量与平面的法向量平行,则直线与平面垂直,我们结合空间直线与直,直线与平面位置关系的判断方法,逐一分析已知中的四个命题,即可得到答案.
解答:解:若
,则b⊥α,故①错误;
若
则,
∥
⇒a∥b,故②正确;
若
,则b∥α,故③正确;
若
,则
∥
,又由b?α,故b⊥α,故④正确;
故选B.
|
若
|
| e1 |
| e2 |
若
|
若
|
| e2 |
| n |
故选B.
点评:本题考查的知识点是向量方法证明线、面位置关系,其中熟练掌握两条直线的方向向量的夹角与直线夹角的关系,直线的方向向量与平面的法向量的夹角与线面夹角的关系,两个平面的法向量的夹角与二面角之间的关系,是解答此类问题的关键.

练习册系列答案
相关题目
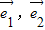 ,平面α的法向量是
,平面α的法向量是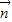 ,
,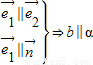 ;②
;②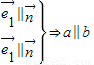 ;③
;③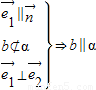 ; ④
; ④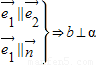 ;
;