摘要：设集合G中的元素是所有形如a+b的数.求证: (1) 当x∈N时, x∈G; (2) 若x∈G.y∈G.则x+y∈G.而不一定属于集合G 证明(1):在a+b中.令a=x∈N,b=0, 则x= x+0*= a+b∈G,即x∈G 证明(2):∵x∈G.y∈G. ∴x= a+b,y= c+d ∴x+y=( a+b)+( c+d)= ∵a∈Z, b∈Z,c∈Z, d∈Z ∴ ∈Z ∴x+y = ∈G. 又∵＝ 且不一定都是整数. ∴＝不一定属于集合G
网址：http://m.1010jiajiao.com/timu_id_4010265[举报]
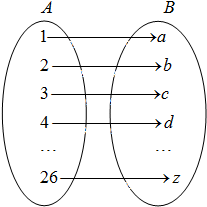设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
|
若f（x1），f[g（20）]，f[g（x2）]，f[g（9）]所表示的字母依次排列组成的英文单词为exam，则x1+x2=
35
35
．
设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
，
若f（x1），f[g（20）]，f[g（x2）]，f[g（9）]所表示的字母依次排列组成的英文单词为exam，则x1+x2= ．
查看习题详情和答案>>
，若f（x1），f[g（20）]，f[g（x2）]，f[g（9）]所表示的字母依次排列组成的英文单词为exam，则x1+x2= ．
查看习题详情和答案>>
，
设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
，