题目内容
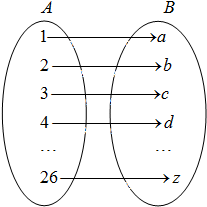设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
|
若f（x1），f[g（20）]，f[g（x2）]，f[g（9）]所表示的字母依次排列组成的英文单词为exam，则x1+x2=
35
35
．分析：由题意知f（x1）=e，f[g（x2）]=a，根据该映射定义可知x1=5，g（x2）=1，再根据g（x）的表达式即可求出x2．从而得到答案．
解答：解：由题意知，f（x1）=e，
由于字母e为第5个英文字母，所以x1=5；
由于f[g（x2）]=a，且字母a为第1个英文字母，所以g（x2）=1，
①当0≤x2≤22时，g（x2）=x2+4=1，解得x2=-3（舍）；
②当22＜x2＜32时，g（x2）=log2（32-x2）=1，解得x2=30；
所以x1+x2=5+30=35．
故答案为：35．
由于字母e为第5个英文字母，所以x1=5；
由于f[g（x2）]=a，且字母a为第1个英文字母，所以g（x2）=1，
①当0≤x2≤22时，g（x2）=x2+4=1，解得x2=-3（舍）；
②当22＜x2＜32时，g（x2）=log2（32-x2）=1，解得x2=30；
所以x1+x2=5+30=35．
故答案为：35．
点评：本题考查映射的定义及函数的求值，考查学生分析问题解决问题的能力．
练习册系列答案
相关题目
设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
，
x+
sinx是否是集合M中的元素，并说明理由；
I都存在x0∈［m,n］,使得等式f(n)-f(m)=(n-m)f′(x0)成立.
，
，