摘要: 已知a.b为正数.求证: (1)若+1>.则对于任何大于1的正数x.恒有ax+>b成立, (2)若对于任何大于1的正数x.恒有ax+>b成立.则+1>. 分析:对带条件的不等式的证明.条件的利用常有两种方法:①证明过程中代入条件,②由条件变形得出要证的不等式. 证明:(1)ax+=a(x-1)++1+a≥2+1+a=(+1)2. ∵+1>(b>0). ∴(+1)2>b.从而ax+>b (2)∵ax+>b对于大于1的实数x恒成立.即x>1时.[ax+]min>b. 而ax+=a(x-1)++1+a≥2+1+a=(+1)2. 当且仅当a(x-1)=.即x=1+>1时取等号. 故[ax+]min=(+1)2. 则(+1)2>b.即+1>. 评述:条件如何利用取决于要证明的不等式两端的差异如何消除. [探索题]已知不等式, 其中n为大于2的整数.表示不超过的最大整数. 设数列的各项为正.且满足 (Ⅰ)证明 (Ⅱ)试确定一个正整数N.使得当时.对任意b>0.都有 解:(Ⅰ)证法1:∵当 即 于是有 所有不等式两边相加可得 由已知不等式知.当n≥3时有. ∵ 证法2:设.首先利用数学归纳法证不等式 (i)当n=3时. 由 知不等式成立. 时.不等式成立.即 则 即当n=k+1时.不等式也成立. 由知. 又由已知不等式得 (Ⅱ)∵ 则有 故取N=1024.可使当n>N时.都有
网址:http://m.1010jiajiao.com/timu_id_4009469[举报]
 >b成立,求证:
>b成立,求证: +1>
+1>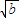 .
.