摘要:若a>0, b>0.且=1, 求证:(I) a+b≥4; (II) 对于一切n∈N*, (a+b)n-an-bn≥22n-2n+1成立 证明:(I) =1, a+b=()(a+b)=1+++1≥4, (II) 当n=1时, 左式=0.右式=0.∴n=1时成立. 假设n=k时成立.即(a+b)k-ak-bk≥22k-2k+1,. 则当n=k+1时.(a+b)k+1-ak+1-bk+1 =(a+b) (a+b)k-ak+1-bk+1 ≥(a+b)(ak+bk+22k-2k+1) -ak+1-bk+1 =abk+bak+(a+b)(22k-2k+1) ≥2·2k+1+4·22k-4·2k+1=22k+2-2k+2, ∴n=k+1时命题成立.归纳原理知,不等式对一切n∈N*都成立
网址:http://m.1010jiajiao.com/timu_id_4009468[举报]
给出下列四个命题:
①若a>b>0,则 >
> ; ②若a>b>0,则a-
; ②若a>b>0,则a- >b-
>b- ; ③若a>b>0,则
; ③若a>b>0,则 >
> ;
;
④若a>0,b>0,且a+b=1,则  的最小值为4.
的最小值为4.
其中正确命题的序号是____ _.(把你认为正确命题的序号都填上)[来源:Zxxk.Com]
查看习题详情和答案>>
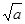 +
+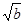 ≤
≤ ;③a2+b2≥2;④a3+b3≥3;⑤
;③a2+b2≥2;④a3+b3≥3;⑤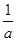 +
+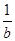 ≥2.
≥2.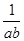 >1
(B)
>1
(B)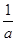 +
+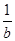 ≤2
≤2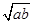 ≥1 (D)a2+b2≥2
≥1 (D)a2+b2≥2