摘要：7． 已知x∈R,求证:ex≥x+1． 证明:设f(x)=ex-x-1,则f′(x)=ex-1． ∴当x=0时.f′(x)=0,f(x)=0． 当x＞0时.f′(x)＞0,∴f(x)在上是增函数．∴f(x)＞f(0)=0． 当x＜0时.f′(x)＜0,f(x)在上是减函数.∴f(x)＞f(0)=0． ∴对x∈R都有f(x)≥0．∴ex≥x+1．
网址：http://m.1010jiajiao.com/timu_id_4009438[举报]
已知f（x）=ln（1+ex）-mx（x∈R）．
（Ⅰ）已知对于给定区间（a，b），存在x0∈（a，b）使得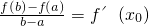
成立，求证：x0唯一；
（Ⅱ）x1，x2∈R，x1≠x2，当m=1时，比较f（
）和
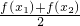大小，并说明理由；
（Ⅲ）设A、B、C是函数f（x）=ln（1+ex）-mx（x∈R，m≥1）图象上三个不同的点，求证：△ABC是钝角三角形．
查看习题详情和答案>>
已知函数f（x）=ex，x∈R．
（Ⅰ） 求f（x）的反函数的图象上的点（1，0）处的切线方程；
（Ⅱ） 证明：曲线y=f（x）与曲线y=
x2+x+1有唯一公共点．
（Ⅲ） 设a＜b，比较f（
）与
的大小，并说明理由．
查看习题详情和答案>>
（Ⅰ） 求f（x）的反函数的图象上的点（1，0）处的切线方程；
（Ⅱ） 证明：曲线y=f（x）与曲线y=
| 1 |
| 2 |
（Ⅲ） 设a＜b，比较f（
| a+b |
| 2 |
| f(b)-f(a) |
| b-a |
已知函数f（x）=ex，x∈R．
（Ⅰ） 求f（x）的反函数的图象上的点（1，0）处的切线方程；
（Ⅱ） 证明：曲线y=f（x）与曲线y=
有唯一公共点．
（Ⅲ） 设a＜b，比较f（
）与
的大小，并说明理由．
查看习题详情和答案>>
（Ⅰ） 求f（x）的反函数的图象上的点（1，0）处的切线方程；
（Ⅱ） 证明：曲线y=f（x）与曲线y=
有唯一公共点．（Ⅲ） 设a＜b，比较f（
）与的大小，并说明理由．查看习题详情和答案>>
成立，求证：x唯一；
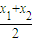）和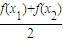
大小，并说明理由；
成立，求证：x唯一；
）和
大小，并说明理由；