Question

已知f（x）=ln（1+e^x）-mx（x∈R）．
（Ⅰ）已知对于给定区间（a，b），存在x∈（a，b）使得成立，求证：x唯一；
（Ⅱ）x₁，x₂∈R，x₁≠x₂，当m=1时，比较f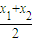（）和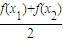大小，并说明理由；
（Ⅲ）设A、B、C是函数f（x）=ln（1+e^x）-mx（x∈R，m≥1）图象上三个不同的点，求证：△ABC是钝角三角形．

Answer 1

【答案】分析：（Ⅰ）假设存在x'，x∈（a，b），且x'≠x，使得f'（x）=f'（x'），由此导出上的单调增函数，从而得到x是唯一的．
（Ⅱ），设，则．由f'（x）单调增．知x＞x₂时，F（x）单调减．x＜x₂时，F（x）单调增，所以．
（Ⅲ）设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），且x₁＜x₂＜x₃，因为m≥1，由，知f（x）是x∈R上的单调减函数由此入手能推导出△ABC为钝角三角形．
解答：解：（Ⅰ）证明：假设存在x'，x∈（a，b），且x'≠x，使得，，
即f'（x）=f'（x'）．（1分）
∵，∴上的单调增函数（或者通过复合函数单调性说明f'（x）的单调性）．（3分）
∴x=x'，这与x'≠x矛盾，即x是唯一的．（4分）
（Ⅱ），原因如下：
设，则．
由（Ⅰ）知f'（x）单调增．
所以当x＞x₂即时，有
所以x＞x₂时，F（x）单调减．（5分）
当x＜x₂即时，有
所以x＜x₂时，F（x）单调增．（6分）
所以F（x）＜F（x₂）=0，所以．（8分）
（Ⅲ）证明：设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），且x₁＜x₂＜x₃，因为m≥1
∵，∴f（x）是x∈R上的单调减函数．（9分）
∴f（x₁）＞f（x₂）＞f（x₃）．∵，
∴．（10分）
∵x₁-x₂＜0，x₃-x₂＞0，f（x₁）-f（x₂）＞0，f（x₃）-f（x₂）＜0，
∴，∴cosB＜0，∠B为钝角．故△ABC为钝角三角形．（12分）
点评：本题考查利用导数判断函数的单调性的综合运用，具有一定的难度，解题时要认真审题，注意题设中的隐含条件，合理地进行等价转换．