摘要:解:先求导数.得 令=0即解得 导数的正负以及.如下表 X -2 -1 0 (0.1) 1 (1.2) 2 y/ 0 + 0 - 0 + y 13 4 5 4 13 从上表知.当时.函数有最大值13.当时.函数有最小值4 在日常生活中.常常会遇到什么条件下可以使材料最省.时间最少.效率最高等问题.这往往可以归结为求函数的最大值或最小值问题. 例2 用边长为60CM的正方形铁皮做一个无盖的水箱.先在四个角分别截去一个小正方形.然后把四边翻转90°角.再焊接而成.问水箱底边的长取多少时.水箱容积最大.最大容积是多少? 例3.已知某商品生产成本C与产量P的函数关系为C=100+4P.价格R与产量P的函数关系为R=25-0.125P.求产量P为何值时.利润L最大.
网址:http://m.1010jiajiao.com/timu_id_4008958[举报]
.在求某些函数的导数时,可以先在解析式两边取对数,再求导数,这比用一般方法求导数更为简单,如求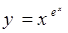 的导数,可先在两边取对数,得
的导数,可先在两边取对数,得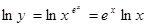 ,再在两边分别对x求导数,得
,再在两边分别对x求导数,得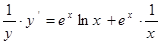 即为
即为 ,即导数为
,即导数为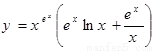 。若根据上面提供的方法计算函数
。若根据上面提供的方法计算函数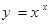 的导数,则
的导数,则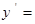 _
_
查看习题详情和答案>>
我们把形如y=f(x
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得lny=lnf(x
=φ(x)lnf(x),两边对x求导数,得
=φ′(x)lnf(x)+φ(x)
,于是y′=f(x
[φ′(x)lnf(x)+φ(x)
],运用此方法可以求得函数y=
(x>0)在(1,1)处的切线方程是
查看习题详情和答案>>
| ) | φ(x) |
| ) | φ(x) |
| y′ |
| y |
| f′(x) |
| f(x) |
| ) | φ(x) |
| f′(x) |
| f(x) |
| x | x |
y=x
y=x
. 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得 ,两边对x求导数,得
,两边对x求导数,得 于是
于是 ,运用此方法可以求得函数
,运用此方法可以求得函数 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .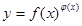 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得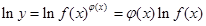 ,两边对
,两边对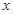 求导数,得
求导数,得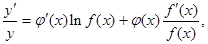 于是
于是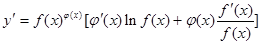 ,运用此方法可以求得函数
,运用此方法可以求得函数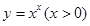 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________