摘要:(一)思想方法总结 1. 数形结合 2. 分类讨论
网址:http://m.1010jiajiao.com/timu_id_4008943[举报]
(此题平行班做)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
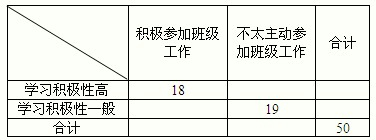
(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是
,请完成上面的2×2列联表;
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
查看习题详情和答案>>
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是
| 12 |
| 25 |
| P(K2≥ko) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
(2012•自贡一模)要研究可导函数f(x)=(1+x)n(n∈N*)在某点x0处的瞬时变化率,有两种方案可供选择:①直接求导,得到f′(x),再把横坐标x0代入导函数f′(x)的表达式;②先把f(x)=(1+x)n按二项式展开,逐个求导,再把横坐标x0代入导函数f′(x)的表达式.综合①②,可得到某些恒等式.利用上述思想方法,可得恒等式:Cn1+2Cn2+3Cn3+…nCnn=
查看习题详情和答案>>
n•2n-1
n•2n-1
n∈N*.我校随机抽取100名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6,
(1)请将上表补充完整(不用写计算过程)
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(3)从学习积极性高的同学中抽取2人继续调查,设积极参加班级工作的人数为X,求X的分布列和期望.
查看习题详情和答案>>
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 40 | ||
| 学习积极性一般 | 30 | ||
| 合计 | 100 |
(1)请将上表补充完整(不用写计算过程)
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(3)从学习积极性高的同学中抽取2人继续调查,设积极参加班级工作的人数为X,求X的分布列和期望.
(2012•普陀区一模)给出问题:已知△ABC满足a•cosA=b•cosB,试判断△ABC的形状,某学生的解答如下:
(i)a•
=b•
?a2(b2+c2-a2)=b2(a2+c2-b2)?(a2-b2)•c2=(a2-b2)(a2+b2)?c2=a2+b2
故△ABC是直角三角形.
(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
故△ABC是等腰三角形.
综上可知,△ABC是等腰直角三角形.
请问:该学生的解答是否正确?若正确,请在下面横线中写出解题过程中主要用到的思想方法;若不正确,请在下面横线中写出你认为本题正确的结果
查看习题详情和答案>>
(i)a•
| b2+c2-a2 |
| 2bc |
| a2+c2-b2 |
| 2ac |
故△ABC是直角三角形.
(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于2RsinAcosA=2RsinBcosB?sin2A=cos2B?A=B
故△ABC是等腰三角形.
综上可知,△ABC是等腰直角三角形.
请问:该学生的解答是否正确?若正确,请在下面横线中写出解题过程中主要用到的思想方法;若不正确,请在下面横线中写出你认为本题正确的结果
等腰或直角三角形
等腰或直角三角形
.