摘要: 复习中.对于排列组合应用题.注意从不同的角度去进行求解.以开阔思维.提高解题能力.
网址:http://m.1010jiajiao.com/timu_id_4008862[举报]
(2011•崇明县二模)已知数列{an}的前n项和为Sn,满足2+2Sn=3an(n∈N*).数列bn=
.
(1)求证:数列{an}为等比数列;
(2)若对于任意n∈N*,不等式bn≥(n+1)λ恒成立,求实数λ的最大值;
(3)对于数列{bn}中值为整数的项,按照原数列中前后顺序排列得到新的数列{cn},记Tn=c1×c3×…×c2n-1,Mn=c2×c4×…×c2n,求
的表达式.
查看习题详情和答案>>
|
(1)求证:数列{an}为等比数列;
(2)若对于任意n∈N*,不等式bn≥(n+1)λ恒成立,求实数λ的最大值;
(3)对于数列{bn}中值为整数的项,按照原数列中前后顺序排列得到新的数列{cn},记Tn=c1×c3×…×c2n-1,Mn=c2×c4×…×c2n,求
| Tn |
| Mn |
(2011•崇明县二模)已知数列{an}的前n项和为Sn,满足2+2Sn=3an(n∈N*).数列bn=
.
(1)求证:数列{an}为等比数列;
(2)若对于任意n∈N*,不等式bn≥(n+1)λ恒成立,求实数λ的最大值;
(3)对于数列{bn}中值为整数的项,按照原数列中前后顺序排列得到新的数列{cn},求数列{cn}的通项公式.
查看习题详情和答案>>
|
(1)求证:数列{an}为等比数列;
(2)若对于任意n∈N*,不等式bn≥(n+1)λ恒成立,求实数λ的最大值;
(3)对于数列{bn}中值为整数的项,按照原数列中前后顺序排列得到新的数列{cn},求数列{cn}的通项公式.
附加题(必做题)
在0,1,2,3,…,9这十个自然数中,任取3个不同的数字.
(1)求组成的三位数中是3的倍数的有多少个?
(2)将取出的三个数字按从小到大的顺序排列,设ξ为三个数字中相邻自然数的组数(例如:若取出的三个数字为0,1,2,则相邻的组为0,1和1,2,此时ξ的值是2),求随机变量ξ的分布列及其数学期望Eξ.
查看习题详情和答案>>
在0,1,2,3,…,9这十个自然数中,任取3个不同的数字.
(1)求组成的三位数中是3的倍数的有多少个?
(2)将取出的三个数字按从小到大的顺序排列,设ξ为三个数字中相邻自然数的组数(例如:若取出的三个数字为0,1,2,则相邻的组为0,1和1,2,此时ξ的值是2),求随机变量ξ的分布列及其数学期望Eξ.
(2012•西城区二模)若An=
(ai=0或1,i=1,2,…,n),则称An为0和1的一个n位排列.对于An,将排列
记为R1(An);将排列
记为R2(An);依此类推,直至Rn(An)=An.对于排列An和Ri(An)(i=1,2,…,n-1),它们对应位置数字相同的个数减去对应位置数字不同的个数,叫做An和Ri(An)的相关值,记作t(An,Ri(An)).例如A3=
,则R1(A3)=
,t(A3,R1(A3))=-1.若t(An,Ri(An))=-1 (i=1,2,…,n-1),则称An为最佳排列.
(Ⅰ)写出所有的最佳排列A3;
(Ⅱ)证明:不存在最佳排列A5;
(Ⅲ)若某个A2k+1(k是正整数)为最佳排列,求排列A2k+1中1的个数.
查看习题详情和答案>>
. |
| a1a2…an |
. |
| ana1a2…an-1 |
. |
| an-1ana1…an-2 |
. |
| 110 |
. |
| 011 |
(Ⅰ)写出所有的最佳排列A3;
(Ⅱ)证明:不存在最佳排列A5;
(Ⅲ)若某个A2k+1(k是正整数)为最佳排列,求排列A2k+1中1的个数.
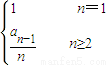 .
.