题目内容
已知数列{an}的前n项和为Sn,满足2+2Sn=3an(n∈N*).数列bn=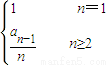 .
.(1)求证:数列{an}为等比数列;
(2)若对于任意n∈N*,不等式bn≥(n+1)λ恒成立,求实数λ的最大值;
(3)对于数列{bn}中值为整数的项,按照原数列中前后顺序排列得到新的数列{cn},求数列{cn}的通项公式.
【答案】分析:(1)由已知中2+2Sn=3an,n∈N*,我们可以得到 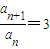 ,根据等比数列的定义,即可得到数列{an}为等比数列;
,根据等比数列的定义,即可得到数列{an}为等比数列;
(2)由(1)中结论,我们易求出数列{bn}的通项公式,下面分类讨论:①当n=1时,b1≥2λ,②n≥2时,令f(n)=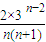 ,利用f(n)=
,利用f(n)=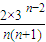 ,(n≥2)为递增数列.f(n)min=
,(n≥2)为递增数列.f(n)min= ,从而λ的最大值.
,从而λ的最大值.
(3)根据当n=2k-1(k≥2)时,及当n=2k(k≥1)时,求出cn的解析式,
解答:解:(1)a1=2,2+2Sn=3an,2+2Sn+1=3an+1,
所以2an+1=3an+1-3an,
即: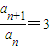 恒成立.
恒成立.
所以,{an}为以2为首项,公比为3的等比数列.
(2)bn=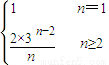 .
.
①n=1时,b1≥2λ,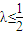
②n≥2时,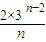 ≥(1+n)λ,λ≤
≥(1+n)λ,λ≤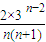
令f(n)=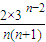 ,f(n+1)-f(n)=
,f(n+1)-f(n)=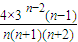 ≥0(n≥2)
≥0(n≥2)
所以,f(n)=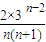 ,(n≥2)为递增数列.f(n)min=
,(n≥2)为递增数列.f(n)min= ,
,
从而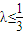
由①,②知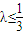 ,所以λ的最大值等于
,所以λ的最大值等于  .
.
(3)c1=1
当n=2k-1(k≥2)时,cn=2×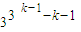
当n=2k(k≥1)时,cn=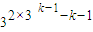
点评:本题以数列递推式为依托,主要考查等比关系的确定,数列的函数特征,数列递推式,数列与不等式的综合.其中(1)的关键是根据等比数列的定义,证得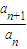 为定值,但要注意由限制首项不为0.
为定值,但要注意由限制首项不为0.
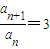 ,根据等比数列的定义,即可得到数列{an}为等比数列;
,根据等比数列的定义,即可得到数列{an}为等比数列;(2)由(1)中结论,我们易求出数列{bn}的通项公式,下面分类讨论:①当n=1时,b1≥2λ,②n≥2时,令f(n)=
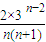 ,利用f(n)=
,利用f(n)=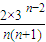 ,(n≥2)为递增数列.f(n)min=
,(n≥2)为递增数列.f(n)min= ,从而λ的最大值.
,从而λ的最大值.(3)根据当n=2k-1(k≥2)时,及当n=2k(k≥1)时,求出cn的解析式,
解答:解:(1)a1=2,2+2Sn=3an,2+2Sn+1=3an+1,
所以2an+1=3an+1-3an,
即:
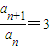 恒成立.
恒成立.所以,{an}为以2为首项,公比为3的等比数列.
(2)bn=
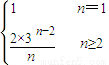 .
.①n=1时,b1≥2λ,
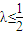
②n≥2时,
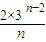 ≥(1+n)λ,λ≤
≥(1+n)λ,λ≤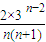
令f(n)=
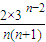 ,f(n+1)-f(n)=
,f(n+1)-f(n)=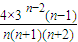 ≥0(n≥2)
≥0(n≥2)所以,f(n)=
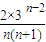 ,(n≥2)为递增数列.f(n)min=
,(n≥2)为递增数列.f(n)min= ,
,从而
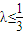
由①,②知
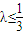 ,所以λ的最大值等于
,所以λ的最大值等于  .
.(3)c1=1
当n=2k-1(k≥2)时,cn=2×
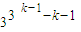
当n=2k(k≥1)时,cn=
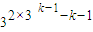
点评:本题以数列递推式为依托,主要考查等比关系的确定,数列的函数特征,数列递推式,数列与不等式的综合.其中(1)的关键是根据等比数列的定义,证得
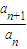 为定值,但要注意由限制首项不为0.
为定值,但要注意由限制首项不为0. 
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |