摘要: 导函数的概念 如果函数在开区间内每一点都可导.就说在内可导.这时.对于开区间内每个确定的值都对应一个确定的导数.这就在内构成一个新的函数.此函数就称为在内的导函数.记作或.即 而当取定某一数值时的导数是上述导函数的一个函数值. 导数与导函数概念不同.导数是在一点处的导数.导函数是某一区间内的导数.对 导函数是以内任一点为自变量.以处的导数值为函数值的函数关系.导函数反映的是一般规律.而等于某一数值时的导数是此规律中的特殊性. [典型例题] [例1] 已知函数在处存在导数.求. 解:上式 令.当时. 上式 [例2] 已知.求导函数 解: 注:利用定义求导数的步骤 (1)求函数增量 (2)求平均变化率 (3)取极限 [例3] 已知曲线C:及点.则过点P可向C引切线条数为( ) A. 0 B. 1 C. 2 D. 3 解:设切点则切线的方程为: 即 由点在直线上.故 或或 所以过点向C可引三条切线 [模拟试题]
网址:http://m.1010jiajiao.com/timu_id_4007992[举报]
导数的概念
(1)对于函数y=f(x),我们把式子![]() 称为函数f(x)从x1到x2的_________.换言之,如果自变量x在x0处有增量Δx,那么函数f(x)相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
称为函数f(x)从x1到x2的_________.换言之,如果自变量x在x0处有增量Δx,那么函数f(x)相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
(2)函数y=f(x)在x=x0处的瞬时变化率是_________,我们称它为函数y=f(x)在x=x0处的_________,记作_________,即![]() (x0)=_________.
(x0)=_________.
(3)函数f(x)的导数![]() (x)就是x的一个函数.我们称它为f(x)的_________,简称_________,记作_________.
(x)就是x的一个函数.我们称它为f(x)的_________,简称_________,记作_________.
导数的概念
(1)对于函数y=f(x),如果自变量x在x0处有增数Δx,那么函数y相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
(2)当Δx→0时,![]() 有极限,我们就说y=f(x)在点x0处_________,并把这个极限叫做f(x)在点x0处的导数(或变化率)记作_________或_________,即
有极限,我们就说y=f(x)在点x0处_________,并把这个极限叫做f(x)在点x0处的导数(或变化率)记作_________或_________,即![]() (x0)=_________=_________,函数f(x)的导数
(x0)=_________=_________,函数f(x)的导数![]() (x)就是当Δx→0时,函数的增量Δy与自变量的增量Δx的比
(x)就是当Δx→0时,函数的增量Δy与自变量的增量Δx的比![]() 的极限,即
的极限,即![]() (x)=_________=_________.
(x)=_________=_________.
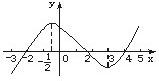
 的定义域为
的定义域为 ,部分对应值如表.
,部分对应值如表. 的图象如图所示.下列关于函数
的图象如图所示.下列关于函数 是周期函数;②函数
是周期函数;②函数 是减函数;③如果当
是减函数;③如果当 时,
时, 的最大值为4;④当
的最大值为4;④当 时,函数
时,函数 有4个零点.其中真命题的个数是 .
有4个零点.其中真命题的个数是 .