区间的概念和记号.求函数定义域的基本方法.求解析式的方法.分段函数,复合函数——青夏教育精英家教网——

摘要：区间的概念和记号.求函数定义域的基本方法.求解析式的方法.分段函数,复合函数

网址：http://m.1010jiajiao.com/timu_id_4006396[举报]

定义区间，，，的长度均为，其中．

（1）求关于的不等式的解集构成的区间的长度；

（2）若关于的不等式的解集构成的区间的长度为，求实数的值；

（3）已知关于的不等式，的解集构成的各区间的长度和超过，求实数的取值范围．

查看习题详情和答案>>

定义区间（m，n），[m，n]，（m，n]，[m，n）的长度均为n-m，其中n＞m．
（1）若关于x的不等式2ax²-12x-3＞0的解集构成的区间的长度为

，求实数a的值；
（2）已知关于x的不等式

，x∈[0，π]的解集构成的各区间的长度和超过

，求实数b的取值范围；
（3）已知关于x的不等式组

的解集构成的各区间长度和为6，求实数t的取值范围．
查看习题详情和答案>>

已知函数

（1）若的极值点，求实数a的值；

（2）若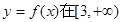上为增函数，求实数a的取值范围；

（3）当有实根，求实数b的最大值。

【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间，求解参数的取值范围，以及利用函数与方程的思想求解参数b的最值。

查看习题详情和答案>>

．
（1）若函数f(x)=min{

(x-1)}，求f（x）表达式
（2）求f(x)=min{3|x-p1|，2×3|x-p2|)}=3|x-p1|，对所有实数x成立的充分必要条件（用p₁，p₂表示）；
（3）若f(x)=min{3|x-p1|，2×3|x-p2|)}，且f（a）=f（b）（a，bp₁，p₂为实数，且a＜bp₁，p₂∈（a，b））求f（x）在区间[a，b]上的单调增区间的长度和（闭区间[m，n]的长度定义为n-m）．

查看习题详情和答案>>

（2009•上海模拟）定义区间（m，n），[m，n]，（m，n]，[m，n）的长度均为n-m，其中n＞m．
（1）若关于x的不等式2ax²-12x-3＞0的解集构成的区间的长度为

，求实数a的值；
（2）求关于x的不等式sinxcosx+

cos2x＞0，x∈[0，2π]的解集构成的各区间的长度和；
（3）已知关于x的不等式组

log2x+log2(tx+3t)＜2

的解集构成的各区间长度和为6，求实数t的取值范围．

查看习题详情和答案>>