摘要:1.区间的概念和记号 在研究函数时,常常用到区间的概念.它是数学中常用的述语和符号. 设a,bR ,且a<b.我们规定: ①满足不等式axb的实数x的集合叫做闭区间.表示为[a,b], ②满足不等式a<x<b的实数x的集合叫做开区间.表示为(a,b), ③满足不等式ax<b 或a<xb的实数x的集合叫做半开半闭区间.分别表示为[a.b) ,(a.b]. 这里的实数a和b叫做相应区间的端点. 在数轴上.这些区间都可以用一条以a和b为端点的线段来表示.在图中.用实心点表示包括在区间内的端点.用空心点表示不包括在区间内的端点: 定 义 名 称 符 号 数 轴 表 示 {x|axb} 闭区间 [a.b] {x|a<x<b} 开区间 (a.b) {x|ax<b} 左闭右开区间 [a.b] {x|a<xb} 左开右闭区间 (a.b) 这样实数集R也可用区间表示为(-,+),“ 读作“无穷大 .“- 读作“负无穷大 .“+ 读作“正无穷大 .还可把满足xa.x>a.xb.x<b的实数x的集合分别表示为[a.+.(a.+),(- ,b,(- ,b). 注意:书写区间记号时: ①有完整的区间外围记号, ②有两个区间端点.且左端点小于右端点, ③两个端点之间用“. 隔开.
网址:http://m.1010jiajiao.com/timu_id_4006388[举报]
已知函数
(1)若 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若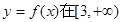 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(3)当 有实根,求实数b的最大值。
有实根,求实数b的最大值。
【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间,求解参数的取值范围,以及利用函数与方程的思想求解参数b的最值。
查看习题详情和答案>>
记min{p,q}=
.
(1)若函数f(x)=min{
,
(x-1)},求f(x)表达式
(2)求f(x)=min{3|x-p1|,2×3|x-p2|)}=3|x-p1|,对所有实数x成立的充分必要条件(用p1,p2表示);
(3)若f(x)=min{3|x-p1|,2×3|x-p2|)},且f(a)=f(b)(a,bp1,p2为实数,且a<bp1,p2∈(a,b))求f(x)在区间[a,b]上的单调增区间的长度和(闭区间[m,n]的长度定义为n-m).
查看习题详情和答案>>
|
(1)若函数f(x)=min{
| x |
| 2 |
| 3 |
(2)求f(x)=min{3|x-p1|,2×3|x-p2|)}=3|x-p1|,对所有实数x成立的充分必要条件(用p1,p2表示);
(3)若f(x)=min{3|x-p1|,2×3|x-p2|)},且f(a)=f(b)(a,bp1,p2为实数,且a<bp1,p2∈(a,b))求f(x)在区间[a,b]上的单调增区间的长度和(闭区间[m,n]的长度定义为n-m).
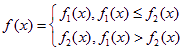 。
。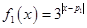 ,
,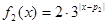 ,
,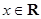 ,
,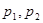 为常
为常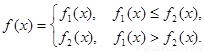
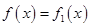 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用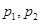 表示);
表示);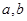 为两实数,
为两实数,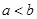 且
且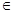
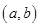 ,若
,若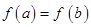
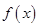 在区间
在区间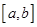 上的单调增区间的长度和为
上的单调增区间的长度和为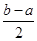 (闭区间
(闭区间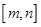 的长度定义为
的长度定义为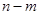 ).
).