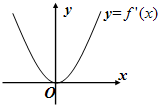已知f（x）是定义域为R的奇函数，f（-4）=-2，f（x）的导函数f′（x）的图象如图所示，若两正数a，b满足f（a+2b）＜2，则

a+4

b+4

的取值范围是（　　）

已知函数f（x）=lnx，g(x)=

1

2

ax2+bx(a≠0)
（1）当a=-2时，函数h（x）=f（x）-g（x）在其定义域内是增函数，求实数b的取值范围；
（2）令V（x）=2f（x）-x²-kx（k∈R），如果V（x）的图象与x轴交于A（x₁，0）、B（x₂，0）两点（0＜x₁＜x₂），且线段AB的中点为C（x₀，0），函数V（x）的导函数为V′（x），求证：V′（x₀）≠0．

已知y=f（x）是R上的可导函数，对于任意的正实数t，都有函数g（x）=f（x+t）-f（x）在其定义域内为减函数，则函数y=f（x）的图象可能为如图中（　　）

定义：设函数y=f（x）在（a，b）内可导，f'（x）为f（x）的导数，f''（x）为f'（x）的导数即f（x）的二阶导数，若函数y=f（x） 在（a，b）内的二阶导数恒大于等于0，则称函数y=f（x）是（a，b）内的下凸函数（有时亦称为凹函数）．已知函数f（x）=xlnx
（1）证明函数f（x）=xlnx是定义域内的下凸函数，并在所给直角坐标系中画出函数f（x）=xlnx的图象；
（2）对?x₁，x₂∈R⁺，根据所画下凸函数f（x）=xlnx图象特征指出x₁lnx₁+x₂lnx₂≥（x₁+x₂）[ln（x₁+x₂）-ln2]与x₁lnx₁+x₂lnx₂≥（x₁+x₂）[ln（x₁+x₂）-ln2]的大小关系；
（3）当n为正整数时，定义函数N （n）表示n的最大奇因数．如N （3）=3，N （10）=5，…．记S（n）=N（1）+N（2）+…+N（2ⁿ），若

2n

i=1

xi=1，证明：

2n

i=1

xilnxi≥-ln2nln

1

3S(n)-2

（i，n∈N^*）．