摘要: 已知直线是的切线.则的值为 .
网址:http://m.1010jiajiao.com/timu_id_4006240[举报]
已知函数f(x)=x3-x2+ax+b的图象在点P(0,f(0))处的切线方程为y=3x-2。
(I)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+ 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。
(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q 的坐标;若不存在,说明理由。
查看习题详情和答案>>
(I)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+
 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q 的坐标;若不存在,说明理由。
已知函数f(x)=lnx-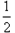 ax2+(a-1)x(a∈R且a≠0),
ax2+(a-1)x(a∈R且a≠0),
(1)求函数f(x)的单调区间;
(2)记函数y=F(x)的图象为曲线C。设点A(x1,y1),B(x2,y2)是曲线C上的不同两点。如果在曲线C上存在点M(x0,y0),使得:①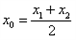 ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”。试问:函数f(x)是否存在“中值相依切线”,请说明理由。
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”。试问:函数f(x)是否存在“中值相依切线”,请说明理由。
查看习题详情和答案>>
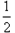 ax2+(a-1)x(a∈R且a≠0),
ax2+(a-1)x(a∈R且a≠0),(1)求函数f(x)的单调区间;
(2)记函数y=F(x)的图象为曲线C。设点A(x1,y1),B(x2,y2)是曲线C上的不同两点。如果在曲线C上存在点M(x0,y0),使得:①
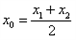 ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”。试问:函数f(x)是否存在“中值相依切线”,请说明理由。
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”。试问:函数f(x)是否存在“中值相依切线”,请说明理由。对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切”;若两直线都与圆相离,则称该位置关系为“平行相离”;否则称为“平行相交”。已知直线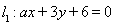 ,
,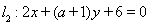 ,和圆C:
,和圆C: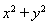
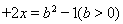 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )
A. 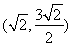 B.
B. 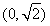
C.  D.
D. 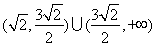
查看习题详情和答案>>
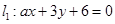 ,
,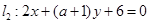 ,和圆C:
,和圆C: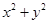
 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )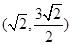
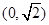
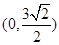

 ,
, ,和圆C:
,和圆C:
 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )


