摘要:存 在 性 探 究 题 例1.如图.在△ABC中.BC=6.AC=.∠ACB=45°.在BC边上有一动点M.过M作MN∥AB.与AC交于点N.连结AM.设BM0<<6.△AMN的面积为.(1)求与的函数关系式, (2)是否存在这样的点M.使=2:3? 若存在则求之.否则说明理由. 例2.已知:如图.在平面直角坐标系中.点C在轴上.以C为圆心.4cm为半径的圆与轴相交于点A.B.与轴相交于D.E.且.点P是⊙C上一动点.连结BP.AP. (1)求∠BPA的度数, (2)若过点P的⊙C的切线交轴于点G.是否存在点P.使△APB与以A.G.P为顶点的三角形相似? 若存在.求出点P的坐标,若不存在.说明理由. 例3. 探索下列问题: (1)在图12-1给出的四个正方形中.各画出一条直线(依次是:水平方向的直线.竖直方向的直线.与水平方向成45°角的直线和任意的直线).将每个正方形都分割成面积相等的两部分, (2)一条竖直方向的直线m以及任意的直线n.在由左向右平移的过程中.将正六边形分成左右两部分.其面积分别记为S1和S2. ①请你在图12-2中相应图形下方的横线上分别填写S1与S2的数量关系式(用“< .“= .“> 连接), ②请你在图12-3中分别画出反映S1与S2三种大小关系的直线n.并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“< .“= .“> 连接). (3)是否存在一条直线.将一个任意的平面图形分割成面积相等的两部分.请简略说出理由.
网址:http://m.1010jiajiao.com/timu_id_4000498[举报]
如图1,已知直线y=kx与抛物线 交于点A(3,6).
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM, 交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值,如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重
合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探
究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
 |
查看习题详情和答案>>
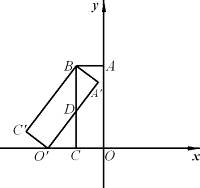
如图,矩形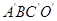 是矩形
是矩形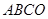 绕点B顺时针旋转得到的.其中点
绕点B顺时针旋转得到的.其中点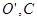 在
在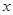 轴负半轴上,线段
轴负半轴上,线段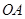 在
在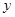 轴正半轴上,
轴正半轴上,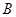 点的坐标为
点的坐标为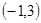 .
.
【小题1】 (1)如果二次函数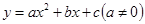 的图象经过
的图象经过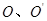 两点且图象顶点
两点且图象顶点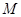 的纵坐标为
的纵坐标为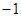 .求这个二次函数的解析式;
.求这个二次函数的解析式;
【小题2】 (2)求边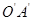 所在直线的解析式;
所在直线的解析式;
【小题3】 (3)在(1)中求出的二次函数图象上是否存在点P,使得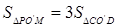 ,若存 在,请求出点P的坐标,若不存在,请说明理由.
,若存 在,请求出点P的坐标,若不存在,请说明理由.
(本小题满分14分)
已知:如图,抛物线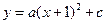 与y轴交于点C(0,
与y轴交于点C(0,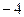 ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
(1)求该抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PD∥BC,交AC于点D,连接CP.当△CPD的面积最大时,求点P的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(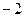 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
 是矩形
是矩形 绕点B顺时针旋转得到的.其中点
绕点B顺时针旋转得到的.其中点 在
在 轴负半轴上,线段
轴负半轴上,线段 在
在 轴正半轴上,
轴正半轴上, 点的坐标为
点的坐标为 .
.
 的图象经过
的图象经过 两点且图象顶点
两点且图象顶点 的纵坐标为
的纵坐标为 .求这个二次函数的解析式;
.求这个二次函数的解析式; 所在直线的解析式;
所在直线的解析式; ,若存 在,请求出点P的坐标,若不存在,请说明理由.
,若存 在,请求出点P的坐标,若不存在,请说明理由.