Question

如图1,已知直线y=kx与抛物线               交于点A（3，6）.

（1）求直线y=kx的解析式和线段OA的长度；

（2）点P为抛物线第一象限内的动点,过点P作直线PM, 交x轴于点M（点M、O不重合）,交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究：线段QM与线段QN的长度之比是否为定值？如果是,求出这个定值,如果不是,说明理由；

（3）如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上（与点O、A不重

合）,点D（m，0）是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探

究：m在什么范围时,符合条件的E点的个数分别是1个、2个？

 

Answer 1

解：（1）把点A（3,6）代入y=kx 得6=3k   ∴k=2       ∴y=2x 

OA= 

（2）是一个定值 ，理由如下：

过点Q作QG⊥y轴于点G，QH⊥x轴于点H .

①当QH与QM重合时，显然QG与QN重合,

此时；

②当QH与QM不重合时，∵QN⊥QM,QG⊥QH

不妨设点H，G分别在x、y轴的正半轴上

∴∠MQH =∠GQN    又∵∠QHM=∠QGN=90°∴△QHM∽△QGN   

∴

当点P、Q在抛物线和直线上不同位置时，同理可得        

（3）延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R

∵∠AOD=∠BAE   ∴AF=OF    ∴OC=AC=OA= 

∵∠ARO=∠FCO=90°   ∠AOR=∠FOC

∴△AOR∽△FOC  ∴  

∴OF=    ∴点F（，0）

设点B（x，），过点B作BK⊥AR于点K，则△AKB∽△ARF

∴ 即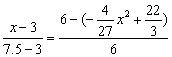   解得x₁=6 ,x₂=3（舍去）

∴点B(6,2)         

∴BK=6－3=3  AK=6－2=4     ∴AB=5         …8分

(求AB也可采用下面的方法)

设直线AF为y=kx＋b（k≠0） 把点A（3,6），点F（，0）代入得

k=，b=10      ∴

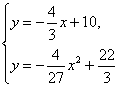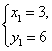 ∴（舍去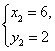）  ∴B（6,2）∴AB=5   …8分

(其它方法求出AB的长酌情给分)

在△ABE与△OED中

∵∠BAE=∠BED    ∴∠ABE＋∠AEB=∠DEO＋∠AEB   ∴∠ABE=∠DEO

∵∠BAE=∠EOD    ∴△ABE∽△OED 

设OE=x，则AE=－x （）   由△ABE∽△OED得 

∴ ∴ （）…10分

∴顶点为（，）

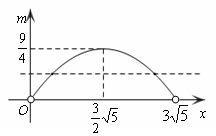
如图，当时，OE=x=,此时E点有1个；当时，任取一个m的值都对应着两个x值，此时E点有2个.

∴当时，E点只有1个 

当时，E点有2个