摘要:利用电路规律求解.主要还是欧姆定律.串并联电路.电功.电热. [例1]如图所示.粗细均匀的金属环的电阻为R.可转动原金属杆OA的电阻为R/4.杆长为L.A端与环相接触.一定值电阻分别与杆的端点O及环边连接.杆OA在垂直于环面向里的.磁感应强度为 B的匀强磁场中.以角速度ω顺时针转动.又定值电阻为R/2.求电路中总电流的变化范围. 解析:设某一时刻金属杆转至图示位置.杆切割磁感线产生感应电动势相当于电源.金属杆上由A沿顺时针方向到D和沿逆时针方向到D的两部分电阻(分别设为Rx和Ry)并联.再与定值电阻R/2串联.组成外电路.等效电路如图所示.则电路中的总电流 I=ε/R总.而ε=LVB=½ωL2B R总=R/4十R并十R/2=3R/4+R并.所以I=½ωL2B/(3R/4+R并) 上式中R并=RxRy/(Rx+Ry).由于Rx+Ry=R为定值.当Rx=Ry时RxRy有最大值.即R并有最大值.此最大值为R/4.所以I的最小为ωL2B/2R.当Rx=0或Ry=0时.R并有最小值零.所以I的最大值为2ωL2B/3R.从而ωL2B/2R≤I≤2ωL2B/3R. [例2]如图所示.半径为a的圆形区域内有匀强磁场.磁感应强度B=0.2 T.磁场方向垂直纸面向里.半径为b的金属圆环与磁场同心地旋转.磁场与环面垂直.其中a=0.4 m,b=0.6m.金属环上分别接有灯L1.L2.两灯的电阻均为R0=2Ω.一金属棒MN与金属环接触良好.棒与环的电阻均不计. (1)若棒以v0=5 m/s的速率在环上向右匀速滑动.求棒滑过圆环直径00'的瞬时,MN中的电动势和流过L1的电流. (2)撤去中间的金属棒MN.将右面的半圆环OL2O/以OO/为轴向上翻转900.若此时磁场随时间均匀变化.其变化率为T/s.求L1的功率. 解析:(1)棒匀速滑动到直径OO/的瞬时.垂直切割磁感线的有效长度为2a,故产生感应电动势E1=B2av0=0.2×2×0.4×5=0.8(V).灯L1 , L2并联电压都为0. 8V,故流过灯L1的电流I1=E/R0=0.4(A) (2)撤去中间的金属棒MN.右面的半圆环OL2O/'以OO/为轴向上翻转900.有效的磁场减为一半.面积为πa2/2,根据法拉第电磁感应定律,此刻电路串联.灯L1的功率 =1.28 ×10-2 W
网址:http://m.1010jiajiao.com/timu_id_4000394[举报]
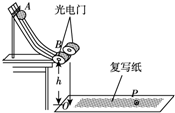 某探究小组利用如图所示装置探究平抛运动中机械能是否守恒.在斜槽轨道的末端安装一个光电门B,调节激光束与球心等高,斜槽末端水平.地面上依次铺有白纸、复写纸,让小球从斜槽上固定位置A点无初速释放,通过光电门后落在地面的复写纸上,在白纸上留下打击印.重复实验多次,测得小球通过光电门的平均时间为2.50ms(毫秒).当地重力加速度为9.8m/s2.
某探究小组利用如图所示装置探究平抛运动中机械能是否守恒.在斜槽轨道的末端安装一个光电门B,调节激光束与球心等高,斜槽末端水平.地面上依次铺有白纸、复写纸,让小球从斜槽上固定位置A点无初速释放,通过光电门后落在地面的复写纸上,在白纸上留下打击印.重复实验多次,测得小球通过光电门的平均时间为2.50ms(毫秒).当地重力加速度为9.8m/s2.(1)小球直径为0.50cm,由此可知小球通过光电门的速度vB=
2.00
2.00
m/s;(2)实验测得轨道离地面的高度h=0.441m,小球的平均落点P到轨道末端正下方O点的距离x=0.591m,则由平抛运动规律解得小球平抛的初速度v0=
1.99
1.99
m/s;(3)在误差允许范围内,实验结果满足小球通过光电门的速度vB与由平抛运动规律求解的平抛初速度v0满足
相等
相等
关系,就可以认为平抛运动过程中机械能是守恒的. 某小组利用如图甲所示装置探究平抛运动中机械能是否守恒.在斜槽轨道的末端安装一个光电门B,调节激光束与球心等高,斜槽末端水平.地面上依次铺有白纸、复写纸,让小球从斜槽上固定位置A点无初速释放,通过光电门后落在地面的复写纸上,在白纸上留下打击印.重复实验多次,测得小球通过光电门的平均时间为2.50ms.当地重力加速度为
某小组利用如图甲所示装置探究平抛运动中机械能是否守恒.在斜槽轨道的末端安装一个光电门B,调节激光束与球心等高,斜槽末端水平.地面上依次铺有白纸、复写纸,让小球从斜槽上固定位置A点无初速释放,通过光电门后落在地面的复写纸上,在白纸上留下打击印.重复实验多次,测得小球通过光电门的平均时间为2.50ms.当地重力加速度为9.8m/s2,计算结果保留三位有效数字.
①用游标卡尺测得小球直径如图乙所示,则小球直径为d=
0.50
0.50
cm,由此可知小球通过光电门的速度vB=2.00
2.00
m/s;②实验测得轨道离地面的高度h=0.441m,小球的平均落点P到轨道末端正下方O点的距离x=0.591m,则由平抛运动规律解得小球平抛的初速度v0=
1.97
1.97
m/s;③在误差允许范围内,实验结果满足小球通过光电门的速度vB与由平抛运动规律求解的平抛初速度v0满足
v0=vB
v0=vB
关系,就可以认为平抛运动过程中机械能是守恒的. 有一种测量物体重量的电子秤,其电路原理图如图中的虚线所示,主要由三部分构成:踏板、压力传感器R(实际上是一个阻值可随压力变化的电阻器)、显示体重的仪表G (实质上是电流表).不计踏板的质量,已知电流表的量程为2A,内阻为1Ω,电源电动势为12V,内阻为1Ω,电阻R随压力F变化的函数式为R=30-0.01F(F和R的单位分别为N和Ω).下列说法中正确的是( )
有一种测量物体重量的电子秤,其电路原理图如图中的虚线所示,主要由三部分构成:踏板、压力传感器R(实际上是一个阻值可随压力变化的电阻器)、显示体重的仪表G (实质上是电流表).不计踏板的质量,已知电流表的量程为2A,内阻为1Ω,电源电动势为12V,内阻为1Ω,电阻R随压力F变化的函数式为R=30-0.01F(F和R的单位分别为N和Ω).下列说法中正确的是( ) 质谱仪是测带电粒子质量和分;析同位素的一种仪器,它的工作原理是带电粒子(不计重力)经同一电场加速后垂直进入同一匀强磁场做圆周运动,然后利用相关规律计算出带电粒子的质量.其工作原理如图所示,虚线为某粒子的运动轨迹,由图可知( )
质谱仪是测带电粒子质量和分;析同位素的一种仪器,它的工作原理是带电粒子(不计重力)经同一电场加速后垂直进入同一匀强磁场做圆周运动,然后利用相关规律计算出带电粒子的质量.其工作原理如图所示,虚线为某粒子的运动轨迹,由图可知( )