摘要:14.从1.2.-.9中任取 n 个数.其中一定可以找到若干个数(至少一个.也可以是全部).它们的和能被10整除.求 n 的最小值. 简答:
网址:http://m.1010jiajiao.com/timu_id_4000134[举报]
在10件产品中,有7件正品,3件次品,现从中任取3件产品,并给出以下结论:
①所取出的3件产品中,有可能3件全是次品.
②所取出的3件产品中,有可能3件全是正品.
③所取出的3件产品中,既有次品也有正品.
④所取出的3件产品中,其正品数一定大于次品数.
其中正确的结论其有
[ ]
A.1个
B.2个
C.3个
D.4个
已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3三个数中任取的一个数,b是从l,2,3,4四个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件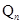 (2≤n≤7,n为整数),则当
(2≤n≤7,n为整数),则当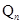 的概率最大时,n的所有可能的值为_
_
的概率最大时,n的所有可能的值为_
_
查看习题详情和答案>>
甲、乙两同学做“射任意球”的游戏,他们商定:每人玩5局,每局在距球门25米处将足球射入空门,一次不进可以射第二次,依次类推,但最多只能射6次,当球射进后,该局结束,并记下射门次数;当6次都未射进,该局也结束,并记为“×”,两人5局射门进球情况如下:
| 第一局 | 第二局 | 第三局 | 第四局 | 第五局 | |
| 甲 | 5次 | × | 4次 | × | 1次 |
| 乙 | × | 2次 | 4次 | 2次 | × |
(1)为了计算得分,双方约定:记“×”的该局为0分,其他局得分的计算方法要满足以下两个条件:①射门次数越多,得分越低;②得分为正数。请你按约定的要求,用公式或文字叙述的方式,选取其中的一种写出一个将其他局的射门次数n换算成得分M的具体方案;
(2)根据上述约定和你写出的方案,请你通过表格的方式,统计甲、乙两人的每局得分和平均分,并从平均分的角度来判断甲、乙两人谁的任意球射门技术更精湛。
查看习题详情和答案>>