摘要:例1 (1)求函数在处的导数. (2)求函数在附近的平均变化率,并求出该点处的导数. 分析: 先求,再求,最后求. 解: 法二 (2) 例2 将原油精炼为汽油.柴油.塑胶等各种不同产品,需要对原油进行冷却和加热,如果第时,原油的温度(单位:)为,计算第时和第时,原油温度的瞬时变化率,并说明它们的意义. 解: 在第时和第时,原油温度的瞬时变化率就是和 根据导数定义 所以 同理可得: 在第时和第时,原油温度的瞬时变化率分别为和, 说明在第附近,原油温度大约以的速率下降 在第附近,原油温度大约以的速率上升. 注: 一般地,反映了原油温度在时刻附近的变化情况.
网址:http://m.1010jiajiao.com/timu_id_4000063[举报]
记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,x0)为坐标的点为函数f(x)图象上的不动点.
(1)若函数f(x)=
图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
(2)设点P(x,y)到直线y=x的距离d=
.在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标yP>3,求点P到直线A1A2距离的最小值及取得最小值时点P的坐标.
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
查看习题详情和答案>>
(1)若函数f(x)=
| 3x+a |
| x+b |
(2)设点P(x,y)到直线y=x的距离d=
| |x-y| | ||
|
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,x0)为坐标的点为函数f(x)图象上的不动点.
(1)若函数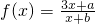 图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
(2)设点P(x,y)到直线y=x的距离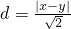 .在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标yP>3,求点P到直线A1A2距离的最小值及取得最小值时点P的坐标.
.在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标yP>3,求点P到直线A1A2距离的最小值及取得最小值时点P的坐标.
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
查看习题详情和答案>>
记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,x0)为坐标的点为函数f(x)图象上的不动点.
(1)若函数f(x)=
图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
(2)设点P(x,y)到直线y=x的距离d=
.在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标yP>3,求点P到直线A1A2距离的最小值及取得最小值时点P的坐标.
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
查看习题详情和答案>>
(1)若函数f(x)=
| 3x+a |
| x+b |
(2)设点P(x,y)到直线y=x的距离d=
| |x-y| | ||
|
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
 .
. 或
或 ?若存在,则举一例说明;若不存在,则证明之.
?若存在,则举一例说明;若不存在,则证明之. 在区间
在区间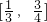 上的最值.(参考公式
上的最值.(参考公式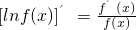 )
)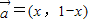
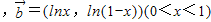 .
. 或
或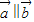 ?若存在,则举一例说明;若不存在,则证明之.
?若存在,则举一例说明;若不存在,则证明之.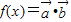 在区间
在区间 上的最值.(参考公式
上的最值.(参考公式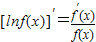 )
)