网址:http://m.1010jiajiao.com/timu_id_3999978[举报]
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集;
内的解集;
(2)若点![]() 是过点
是过点![]() 且法向量为
且法向量为![]() 的直线
的直线![]() 上的动点.当
上的动点.当![]() 时,设函数
时,设函数![]() 的值域为集合
的值域为集合![]() ,不等式
,不等式![]() 的解集为集合
的解集为集合![]() . 若
. 若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数![]() 的性质取决于变量
的性质取决于变量![]() 、
、![]() 和
和![]() 的值. 当
的值. 当![]() 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
.
(1)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(2)若点 是过点
是过点 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在 处
处 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
.
(1)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(2)若点 是过点
是过点 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在 处
处 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
查看习题详情和答案>>
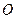 为坐标原点,点
为坐标原点,点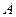 的坐标为
的坐标为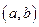 ,点
,点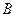 的坐标为
的坐标为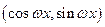 ,其中
,其中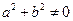 且
且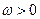 .设
.设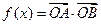 .
.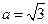 ,
,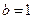 ,
,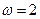 ,求方程
,求方程 在区间
在区间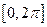 内的解集;
内的解集;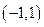 且法向量为
且法向量为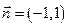 的直线
的直线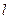 上的动点.当
上的动点.当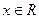 时,设函数
时,设函数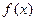 的值域为集合
的值域为集合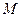 ,不等式
,不等式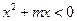 的解集为集合
的解集为集合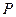 . 若
. 若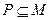 恒成立,求实数
恒成立,求实数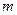 的最大值;
的最大值;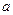 、
、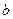 和
和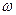 的值. 当
的值. 当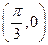 对称,且在
对称,且在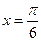 处
处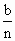 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.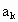 (1≤k≤n)为第A位职工所得奖金额,试求
(1≤k≤n)为第A位职工所得奖金额,试求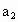 ,
,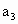 ,并且用无,n和b表示
,并且用无,n和b表示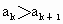 (k=l,2,…,n-1),并解释此不等式关于分配原则的实际意义.
(k=l,2,…,n-1),并解释此不等式关于分配原则的实际意义.