摘要：设斜率为1的直线过抛物线()的焦点F,且和x轴交于点P,若△OPF(O为坐标原点) 的面积为2,则 = ．
网址：http://m.1010jiajiao.com/timu_id_3995966[举报]
如图，斜率为1的直线过抛物线
的焦点F，与抛物线交于两点A，B，
（1）若|AB|=8，求抛物线
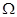的方程；
（2）设C为抛物线弧AB上的动点（不包括A，B两点），求
的面积S的最大值；
（3）设P是抛物线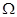上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）
查看习题详情和答案>>
如图，斜率为1的直线
过抛物线
的焦点F，与抛物线交于两点A，B。
（1）若|AB|=8，求抛物线
的方程；
（2）设P是抛物线上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）。
查看习题详情和答案>>
如图，斜率为1的直线过抛物线
的焦点F，与抛物线交于两点A，B，
（1）若|AB|=8，求抛物线
的方程；
（2）设C为抛物线弧AB上的动点（不包括A，B两点），求
的面积S的最大值；
（3）设P是抛物线上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）
的焦点F，与抛物线交于两点A，B，
的方程；
的面积S的最大值；
如图，斜率为1的直线过抛物线Ω：y2=2px（p＞0）的焦点F，与抛物线交于两点A，B，