摘要:分类原则:分类对象确定.标准统一.不重复.不遗漏.分层次.不越级讨论.
网址:http://m.1010jiajiao.com/timu_id_3994034[举报]
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
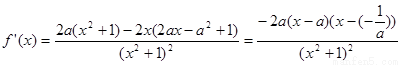 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当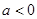 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 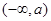 ,
,

 ,
, 
查看习题详情和答案>>
我们用min{S1,S2,…,Sn}和max{S1,S2,…,Sn}分别表示实数S1,S2,…,Sn中的最小者和最大者.
(1)设f(x)=min{sinx,cosx},g(x)=max{sinx,cosx},x∈[0,2π],函数f(x)的值域为A,函数g(x)的值域为B,求A∩B;
(2)数学课上老师提出了下面的问题:设a1,a2,an为实数,x∈R,求函数![]() (x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
(x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数![]() 和
和![]() 的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
