网址:http://m.1010jiajiao.com/timu_id_3993948[举报]
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当 时,
时, ,令
,令 得
得
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
查看习题详情和答案>>
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1, f(x1)),B(x2, f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
当 时
时 单调递减;当
单调递减;当 时
时 单调递增,故当
单调递增,故当 时,
时, 取最小值
取最小值
于是对一切 恒成立,当且仅当
恒成立,当且仅当 . ①
. ①
令 则
则
当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减.
单调递减.
故当 时,
时, 取最大值
取最大值 .因此,当且仅当
.因此,当且仅当 时,①式成立.
时,①式成立.
综上所述, 的取值集合为
的取值集合为 .
.
(Ⅱ)由题意知, 令
令 则
则


令 ,则
,则 .当
.当 时,
时, 单调递减;当
单调递减;当 时,
时, 单调递增.故当
单调递增.故当 ,
, 即
即
从而 ,
, 又
又

所以
 因为函数
因为函数 在区间
在区间 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在 使
使 即
即 成立.
成立.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出 取最小值
取最小值 对一切x∈R,f(x)
对一切x∈R,f(x)  1恒成立转化为
1恒成立转化为 从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
查看习题详情和答案>>
研究问题:“已知关于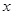 的不等式
的不等式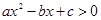 的解集为(1,2),解关于
的解集为(1,2),解关于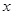 的
的
不等式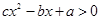 ”,有如下解法:由
”,有如下解法:由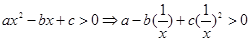 ,令
,令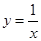 ,则
,则
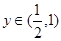 ,所以不等式
,所以不等式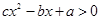 的解集为
的解集为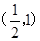 。类比上述解法,已知关于
。类比上述解法,已知关于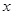 的不等式
的不等式
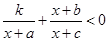 的解集为
的解集为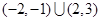 ,则关于
,则关于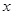 的不等式
的不等式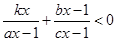 的解集
的解集
为 .
查看习题详情和答案>>
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。





 单调递减
单调递减 的不等式
的不等式 的解集为
的解集为 ,解关于
,解关于 ”,有如下解法:
”,有如下解法:
 ,令
,令 ,则
,则 ,
, .
. 的解集为
的解集为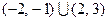 ,求关于
,求关于 的解集.
的解集.