网址:http://m.1010jiajiao.com/timu_id_3993862[举报]
设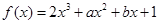 的导数为
的导数为 ,若函数
,若函数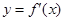 的图象关于直线
的图象关于直线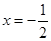 对称,且
对称,且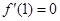 .
.
(Ⅰ)求实数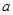 ,
, 的值;
的值;
(Ⅱ)求函数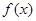 的单调区间.
的单调区间.
【解析】第一问中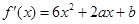 ,由于函数
,由于函数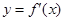 的图象关于直线
的图象关于直线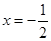 对称,所以
对称,所以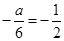
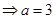 .
.
又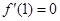
 ∴
∴
第二问中由(Ⅰ), ,
,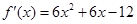
令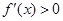
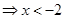 ,或
,或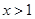 ;
;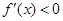

∴函数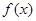 在
在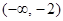 及
及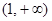 上递增,在
上递增,在 上递减.
上递减.
查看习题详情和答案>>
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
查看习题详情和答案>>