题目内容
设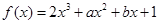 的导数为
的导数为 ,若函数
,若函数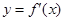 的图象关于直线
的图象关于直线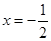 对称,且
对称,且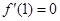 .
.
(Ⅰ)求实数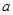 ,
, 的值;
的值;
(Ⅱ)求函数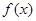 的单调区间.
的单调区间.
【解析】第一问中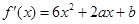 ,由于函数
,由于函数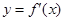 的图象关于直线
的图象关于直线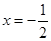 对称,所以
对称,所以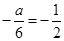
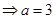 .
.
又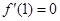
 ∴
∴
第二问中由(Ⅰ), ,
,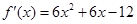
令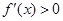
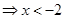 ,或
,或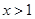 ;
;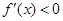

∴函数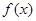 在
在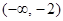 及
及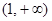 上递增,在
上递增,在 上递减.
上递减.
【答案】
(Ⅰ)  (Ⅱ)函数
(Ⅱ)函数 在
在 及
及 上递增,在
上递增,在 上递减.
上递减.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 的导数为
的导数为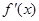 ,若函数
,若函数 的图像关于直
的图像关于直 对称,且
对称,且 . (1)求实数
. (1)求实数 的值 ;(2)求函数
的值 ;(2)求函数 的极值.
的极值.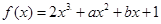 的导数为
的导数为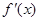 ,若函数
,若函数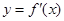 的图像关于直线
的图像关于直线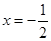 对称,且
对称,且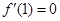 .
.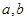 的值(Ⅱ)求函数
的值(Ⅱ)求函数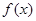 的极值
的极值 的导数为
的导数为 ,若
,若 的图象关于直线
的图象关于直线 对称,且在
对称,且在 处取得极小值
处取得极小值
 的值;
的值; 在
在 的最值
的最值