摘要:求含有两个变量的线性式子的最值.可以构造直线方程.利用截距的意义解决问题.这一应用在线性规划中体现的很充分---求线性目标函数的最值. 例5.已知x,y满足条件=1.求y-3x的最小值和最大值 解:令y-3x=b, 即y=3x+b 由联立可得: 169+966y+16b-400=0,令⊿≥0得: -13≤b≤13 ∴y-3x的最小值和最大值分别是-13和13.
网址:http://m.1010jiajiao.com/timu_id_3993614[举报]
以下说法中正确的是
① 甲乙两同学各自独立地考察了两个变量 的线性相关关系时,发现两个人对
的线性相关关系时,发现两个人对 的观测数据的平均值相等,都是
的观测数据的平均值相等,都是 。对
。对 的观测数据的平均值也相等,都是
的观测数据的平均值也相等,都是 。各自求出的回归直线分别是
。各自求出的回归直线分别是 ,则直线
,则直线 必定相交于定点
必定相交于定点 。
。
②用独立性检验(2×2列联表法)来考察两个分类变量 是否有关系时,算出的随机变量
是否有关系时,算出的随机变量 的值越大,说明“
的值越大,说明“ 有关系”成立的可能性越大。
有关系”成立的可能性越大。
③合情推理就是正确的推理。
④最小二乘法的原理是使得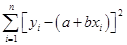 最小。
最小。
⑤用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合程度越好。
越小,说明模型的拟合程度越好。
查看习题详情和答案>>
甲、乙两同学各自独立地考察两个变量 的线性相关关系时,发现两人对
的线性相关关系时,发现两人对 的观察数据的平均值相等,都是
的观察数据的平均值相等,都是 ,对
,对 的观察数据的平均值也相等,都是
的观察数据的平均值也相等,都是 ,各自求出的回归直线分别是
,各自求出的回归直线分别是 ,则直线与必过同一点____________
,则直线与必过同一点____________
查看习题详情和答案>>
商品零售商要了解每周的广告费及消费额(单位:万元)之间的关系,记录如下:
| 广告费(x) | 40 | 28 | 33 | 36 | 25 | 43 | 38 | 30 | 50 | 20 | 42 | 46 |
| 销售额(y) | 490 | 395 | 420 | 475 | 385 | 525 | 480 | 400 | 560 | 365 | 510 | 540 |
利用上述资料:
画出散点图;
求销售额y对广告费x的一元线性回归方程;
求出两个变量的相关系数。
查看习题详情和答案>>
商品零售商要了解每周的广告费及消费额(单位:万元)之间的关系,记录如下:
|
广告费x |
40 |
28 |
33 |
36 |
25 |
43 |
38 |
30 |
50 |
20 |
42 |
46 |
|
销售额y |
490 |
395 |
420 |
475 |
385 |
525 |
480 |
400 |
560 |
365 |
510 |
540 |
利用上述资料:
(1)画出散点图;
(2)求销售额y对广告费x的一元线性回归方程;
(3)求出两个变量的相关系数。
查看习题详情和答案>>