摘要：分式型的最值问题可以通过变形,利用斜率公式解决. 例3．函数y=最大值是 .最小值是 . 解:函数解析式表示经过A两点连线的斜率k.A在单位圆x+y=1上.经过A和B两点的直线方程为y-3=k(x-2) 即kx-y+3-2k=0,由直线和圆的位置关系得≤1解之可得; ≤k≤ 所以函数得最大值是最小值是.
网址：http://m.1010jiajiao.com/timu_id_3993612[举报]
（2006•宝山区二模）给出函数f(x)=
+tx（x∈R）．
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
时，可以将f（x）化成f(x)=a(
+x)+b(
-x)的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
+h(x)，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
| x2+4 |
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
| 1 |
| 2 |
| x2+4 |
| x2+4 |
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
| g(x) |
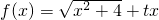（x∈R）
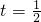时，可以将f（x）化成
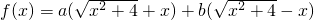的形式，运用基本不等式求f（x）的最小值及此时x的取值；
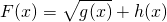，利用基本不等式研究函数F（x）的最值问题．
，函数
（其中
为自然对数的底数）．
在区间
上的最小值；
的通项
，
是前
项和，证明：
．
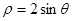上任意一点，求点A到直线
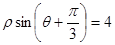的距离的最小值．
上任意一点，求点A到直线
的距离的最小值．