摘要：如图所示.过圆O外一点M作它的一条切线.切点为A.过A点作直线AP垂直于直线OM.垂足为P. (1)证明:OM·OP=OA2, (2)N为线段AP上一点.直线NB垂直于直线ON.且交圆O于B点.过B点的切线交直线ON于K. 证明:∠OKM=90°. 证明 (1)因为MA是圆O的切线,所以OA⊥AM. 又因为AP⊥OM,在Rt△OAM中,由射影定理知, OA2=OM·OP. (2)因为BK是圆O的切线.BN⊥OK. 同(1).有OB2=ON·OK.又OB=OA. 所以OP·OM=ON·OK.即=. 又∠NOP=∠MOK. 所以△ONP∽△OMK.故∠OKM=∠OPN=90°.
网址：http://m.1010jiajiao.com/timu_id_3990842[举报]
已知点P1（a1，b1），P2（a2，b2），…，Pn（an，bn）（n为正整数）都在函数y=(
)x的图象上，且数列{an} 是a1=1，公差为d的等差数列．
（1）证明：数列{bn} 是等比数列；
（2）若公差d=1，以点Pn的横、纵坐标为边长的矩形面积为cn，求最大的实数t，使cn≤
（t∈R，t≠0）对一切正整数n恒成立；
（3）对（2）中的数列{an}，对每个正整数k，在ak与ak+1之间插入3k-1个3（如在a1与a2之间插入30个3，a2与a3之间插入31个3，a3与a4之间插入32个3，…，依此类推），得到一个新的数列{dn}，设Sn是数列{dn}的前n项和，试探究2008是否为数列{Sn}中的某一项，写出你探究得到的结论并给出证明． 查看习题详情和答案>>
| 1 |
| 2 |
（1）证明：数列{bn} 是等比数列；
（2）若公差d=1，以点Pn的横、纵坐标为边长的矩形面积为cn，求最大的实数t，使cn≤
| 1 |
| t |
（3）对（2）中的数列{an}，对每个正整数k，在ak与ak+1之间插入3k-1个3（如在a1与a2之间插入30个3，a2与a3之间插入31个3，a3与a4之间插入32个3，…，依此类推），得到一个新的数列{dn}，设Sn是数列{dn}的前n项和，试探究2008是否为数列{Sn}中的某一项，写出你探究得到的结论并给出证明． 查看习题详情和答案>>
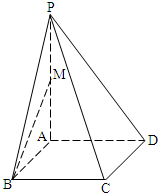（2008•嘉定区一模）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，PA⊥平面ABCD，PC与平面ABCD所成角的大小为arctan2，M为PA的中点．（1）求四棱锥P-ABCD的体积；
（2）求异面直线BM与PC所成角的大小（结果用反三角函数表示）．
某地2008年降雨量p（x）与时间X的函数图象如图所示，定义“落量差函数”q（x）为时间段[0，x]内的最大降雨量与最小降雨量的差，则函数q（x）的图象可能是（ ）
如图，卫星和地面之间的电视信号沿直线传播，电视信号能够传送到达的地面区域，称为这个卫星的覆盖区域．为了转播2008年北京奥运会，我国发射了“中星九号”广播电视直播卫星，它离地球表面的距离约为36000km．已知地球半径约为6400km，则“中星九号”覆盖区域内的任意两点的球面距离的最大值约为