摘要：如图所示.轻弹簧的一端固定.另一端与滑块B相连.B静止在水平直导轨上.弹簧处在原长状态.另一质量与B相同的滑块A,从导轨上的P点以某一初速度向B滑行.当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A.B紧贴在一起运动,但互不粘连.已知最后A恰好 返回到出发点P并停止.滑块A和B与导轨的动摩擦因数都为μ,运动过 程中弹簧最大形变量为l2,重力加速度为g.求A从P点出发时的初速度v0. 答案 解析 令A.B质量皆为m,A刚接触B时速度为v1,由功能关系有: mv02-mv12=μmgl1 ① A.B碰撞过程中动量守恒,令碰后A.B共同运动的速度为v2,有 mv1=2mv2 ② 碰后,A.B先一起向左运动,接着A.B一起被弹回,当弹簧恢复到原长时,设A.B的共同速度为v3,在这过程中,弹簧势能始末两态都为零,利用功能关系,有 ×2mv22-×2mv32=2m×2l2μg ③ 此后A.B开始分离,A单独向右滑到P点停下,由功能关系有 mv32=μmgl1 ④ 由以上①②③④式,解得v0=
网址：http://m.1010jiajiao.com/timu_id_3990636[举报]
（2004?广东）一杂技演员，用一只手抛球．他每隔0.40s抛出一球，接到球便立即把球抛出，已知除抛、接球的时刻外，空中总有四个球，将球的运动看作是竖直方向的运动，球到达的最大高度是（高度从抛球点算起，取g=10m/s2）（ ）
查看习题详情和答案>>
（2004?广东）已经证实，质子、中子都是由上夸克和下夸克的两种夸克组成的，上夸克带电为
e，下夸克带电为-
e，e为电子所带电量的大小，如果质子是由三个夸克组成的，且各个夸克之间的距离都为l，l=1.5×10-15m，试计算质子内相邻两个夸克之间的静电力（库仑力）
查看习题详情和答案>>
| 2 |
| 3 |
| 1 |
| 3 |
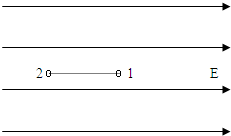（2004?广东）在场强为E的匀强电场中固定放置两个小球1和2，它们的质量相等，电荷分别为q1和q2（q1≠q2）．球1和球2的连线平行于电场线，如图．现同时放开1球和2球，于是它们开始在电场力的作用下运动，如果球1和球2之间的距离可以取任意有限值，则两球刚被放开时，它们的加速度可能是（ ）
（2004?广东）三个完全相同的物块1、2、3放在水平桌面上，它们与桌面间的动摩擦因数都相同．现用大小相同的外力F沿图示方向分别作用在1和2上，用