摘要: 设函数其中..当且仅当时.函数取得最小值. (Ⅰ)求函数的表达式, (Ⅱ)若方程至少有两个不相同的实数根.求取值的集合. 解:(Ⅰ) (Ⅱ)记方程①:方程②: 分别研究方程①和方程②的根的情况: (1)方程①有且仅有一个实数根方程①没有实数根 (2)方程②有且仅有两个不相同的实数根.即方程有两个不相同的非正实数根. 方程②有且仅有一个不相同的实数根.即方程有且仅有一个蜚 正实数根. 综上可知:当方程有三个不相同的实数根时. 当方程有且仅有两个不相同的实数根时. 符合题意的实数取值的集合为
网址:http://m.1010jiajiao.com/timu_id_3988834[举报]
设函数f(x)=-cos2x-4t•sin
cos
+2t2-6t+2(x∈R),其中t∈R,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)当-1≤t≤1时,要使关于t的方程g(t)=kt有且仅有一个实根,求实数k的取值范围 查看习题详情和答案>>
| x |
| 2 |
| x |
| 2 |
(1)求g(t)的表达式;
(2)当-1≤t≤1时,要使关于t的方程g(t)=kt有且仅有一个实根,求实数k的取值范围 查看习题详情和答案>>
设函数f(x)=
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个零点,求实数a取值的集合.
查看习题详情和答案>>
|
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个零点,求实数a取值的集合.
设函数 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个零点,求实数a取值的集合.
查看习题详情和答案>>
 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个零点,求实数a取值的集合.
查看习题详情和答案>>
 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.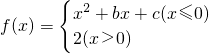 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.