摘要: 已知函数.定义数列.使:.-.- . (1)求证:数列是等差数列, (2)设数列的前n项和为.求证:. 解:(1)∵ ∴ ∴ 又 ∴数列{}是以为首项.以为公差的等差数列. 可知 ∴ ∴ . 19:如图.一张平行四边形的硬纸片中...沿它的对角线把折起.使点到达平面外点的位置. (Ⅰ)证明:平面平面, (Ⅱ)如果△为等腰三角形.求二面角的大小. 解:(Ⅰ)证明:因为. .所以. 因为折叠过程中.. 所以.又.故平面. 又平面. 所以平面平面. (Ⅱ)解法一:如图.延长到.使.连结.. 因为....所以为正方形.. 由于.都与平面垂直.所以.可知. 因此只有时.△为等腰三角形. 在△中..又. 所以△为等边三角形.. 由(Ⅰ)可知..所以为二面角的平面角.即二面角的大小为. 解法二:以为坐标原点.射线.分别为轴正半轴和轴正半轴.建立如图的空间直角坐标系.则... 由(Ⅰ)可设点的坐标为.其中.则有. ① 因为△为等腰三角形.所以或. 若.则有. 则此得..不合题意. 若.则有. ② 联立①和②得..故点的坐标为. 由于..所以与夹角的大小等于二面角的大小. 又.. 所以 即二面角的大小为.
网址:http://m.1010jiajiao.com/timu_id_3988833[举报]
 ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由. ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.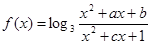 ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使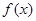 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在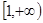 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.