(2005山东，22)如下图,已知动圆过定点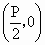，且与直线相切，其中p＞0，

(1)求动圆圆心的轨迹C的方程；

(2)设A、B是轨迹C上异于原点O的两个不同点，直线OA和OB的倾斜角分别为α和β，当α、β变化且α+β为定值θ(0＜θ＜π)时，证明：直线AB恒过定点，并求出该定点的坐标．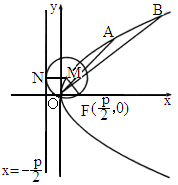

 （选做题）从A，B，C，D四个中选做2个，每题10分，共20分．解答时应写出文字说明、证明过程或演算步骤．

A．（本小题为选做题，满分10分）

如图，AB是半圆的直径，C是AB延长线上一点，CD

切半圆于点D，CD=2，DE⊥AB，垂足为E，且E是

OB的中点，求BC的长．

B．（本小题为选做题，满分10分）

已知矩阵，其中，若点P（1,1）在矩阵A的变换下得到点，

（1）求实数a的值；    （2）求矩阵A的特征值及特征向量.

C．（本小题为选做题，满分10分）

设点分别是曲线和上的动点，求动点间的最小距离.

D．（本小题为选做题，满分10分）

设为正数，证明：≥.