摘要：1．了解导数的概念.能利用导数定义求导数．掌握函数在一点处的导数的定义和导数的几何意义.理解导函数的概念．了解曲线的切线的概念．在了解瞬时速度的基础上抽象出变化率的概念． 2熟记基本导数公式(c,x .sin x, cos x, e, a, lnx, logx的导数).掌握两个函数四则运算的求导法则和复合函数的求导法则.会求某些简单函数的导数.利能够用导数求单调区间.求一个函数的最大(小)值的问题.掌握导数的基本应用．
网址：http://m.1010jiajiao.com/timu_id_3986152[举报]
导数的概念
(1)对于函数y＝f(x)，我们把式子
称为函数f(x)从x1到x2的_________．换言之，如果自变量x在x0处有增量Δx，那么函数f(x)相应地有增量_________；比值_________就叫做函数y＝f(x)在x0到x0＋Δx之间的_________．
(2)函数y＝f(x)在x＝x0处的瞬时变化率是_________，我们称它为函数y＝f(x)在x＝x0处的_________，记作_________，即
(x0)＝_________．
(3)函数f(x)的导数(x)就是x的一个函数．我们称它为f(x)的_________，简称_________，记作_________．
导数的概念
(1)对于函数y＝f(x)，如果自变量x在x0处有增数Δx，那么函数y相应地有增量_________；比值_________就叫做函数y＝f(x)在x0到x0＋Δx之间的_________．
(2)当Δx→0时，
有极限，我们就说y＝f(x)在点x0处_________，并把这个极限叫做f(x)在点x0处的导数(或变化率)记作_________或_________，即
(x0)＝_________＝_________，函数f(x)的导数(x)就是当Δx→0时，函数的增量Δy与自变量的增量Δx的比的极限，即(x)＝_________＝_________．
为平面直角坐标系
中的一个动点（其中O为坐标原点），点P到定点
的距离比点P到
轴的距离大
。
与点P的轨迹相交于A、B两点，且
，求
的值。
是曲线C上的一点，求以Q为切点的曲线C 的切线方程。
为平面直角坐标系
中的一个动点（其中O为坐标原点），点P到定点
的距离比点P到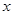
轴的距离大
。
与点P的轨迹相交于A、B两点，且
，求
的值。
是曲线C上的一点，求以Q为切点的曲线C 的切线方程。