摘要：26．如图17.点A是△ABC和△ADE的公共顶点.∠BAC+∠DAE＝180°.AB＝k·AE.AC＝k·AD.点M是DE的中点.直线AM交直线BC于点N． ⑴探究∠ANB与∠BAE的关系.并加以证明． 说明:如果你经过反复探索没解决问题.可以从下面①②中选取一个作为已知条件.再完成你的证明.选取①比选原题少得2分.选取②比选原题少得5分． ① 如图18.k＝1,②如图19.AB＝AC． ⑵若△ADE绕点A旋转.其他条件不变.则在旋转的过程中⑴的结论是否发生变化?如果没有发生变化.请写出一个可以推广的命题,如果有变化.请画出变化后的一个图形.并直接写出变化后∠ANB与∠BAE的关系．
网址：http://m.1010jiajiao.com/timu_id_3983044[举报]
如图1，已知C、D是双曲线y=
在第一象限内的分支上两点，直线CD分别交x轴、y轴于A、B，CG⊥x轴于G，DH⊥x轴于H，
=
=
，OC=
．
（1）求m的值和D点的坐标；
（2）在双曲线第一象限内的分支上是否有一点P，使得S△POC=S△POD？若存在，求出P点坐标；若不存在，请说明理由．
（3）如图2，点K是双曲线y=
在第三象限内的分支上的一动点，过点K作KM⊥y轴于M，OE平分∠KOA，KE⊥OE，KE交y轴于N，直线ME交x轴于F，①
，②
，有一个为定值，请你选择正确结论并求出这个定值．
查看习题详情和答案>>
| m |
| x |
| OG |
| GC |
| DH |
| OH |
| 1 |
| 4 |
| 17 |
（1）求m的值和D点的坐标；
（2）在双曲线第一象限内的分支上是否有一点P，使得S△POC=S△POD？若存在，求出P点坐标；若不存在，请说明理由．
（3）如图2，点K是双曲线y=
| m |
| x |
| OF2+MN2 |
| ON2 |
| OF+MN |
| ON |
如图，⊙O的半径是10cm，点A在⊙O上，线段AC交⊙O于点B，AC=23cm，AB=12cm，点P在线
段AC上，设AP=x（cm），OP=y（cm）．
（1）求y关于x的函数关系式，及x的取值范围；
（2）当x=4、14时，求y的值；
（3）当y=8时，求x的值；
（4）当x为何值时，10≤y≤17？
查看习题详情和答案>>
段AC上，设AP=x（cm），OP=y（cm）．（1）求y关于x的函数关系式，及x的取值范围；
（2）当x=4、14时，求y的值；
（3）当y=8时，求x的值；
（4）当x为何值时，10≤y≤17？
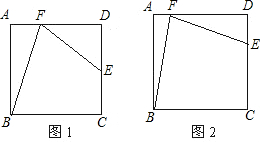
如图1，四边形ABCD是正方形，点E和点F分别在CD和DA上，且∠CBF=∠EFB
（1）小方同学发现，当E为CD的中点时，tan∠ABF=
，当DE=
CD时，tan∠ABF=
，当DE=
CD时，tan∠ABF=
，那么当DE=
CD时，tan∠ABF= ．
（2）如图2，当DE=
CD时，tan∠ABF= ．证明你的猜测的正确性．
查看习题详情和答案>>
（1）小方同学发现，当E为CD的中点时，tan∠ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 5 |
（2）如图2，当DE=
| 1 |
| k+1 |
查看习题详情和答案>>
图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为－3．
图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为－3．