题目内容
如图1,四边形ABCD是正方形,点E和点F分别在CD和DA上,且∠CBF=∠EFB(1)小方同学发现,当E为CD的中点时,tan∠ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 5 |
(2)如图2,当DE=
| 1 |
| k+1 |
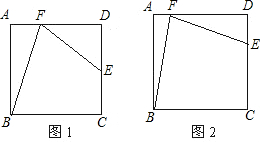
分析:(1)观察题干给出的信息可以发现:可以发现当DE=
CD时,tan∠ABF=
,根据此规律即可求得当DE=
CD时,tan∠ABF的值;
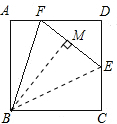
(2)作BM⊥EF于点M,连接BE.分别求证△AFB≌△MFB,△BCE≌△BME,得出AF=FM,AB=BM,EC=EM,
然后设DE=1,FM=a,利用勾股定理即可求得答案.
| 1 |
| n |
| 1 |
| n+(n-1) |
| 1 |
| 5 |
(2)作BM⊥EF于点M,连接BE.分别求证△AFB≌△MFB,△BCE≌△BME,得出AF=FM,AB=BM,EC=EM,
然后设DE=1,FM=a,利用勾股定理即可求得答案.
解答:解:(1)当E为CD的中点时,即当DE=
CD时,tan∠ABF=
=
;
当DE=
CD时,tan∠ABF=
=
;
当DE=
CD时,tan∠ABF=
=
;
…
可以发现当DE=
CD时,tan∠ABF=
;
那么当DE=
CD时,tan∠ABF=
=
.
故答案为:
.
(2)
.
作BM⊥EF于点M,连接BE.
∵AD∥BC,
∴∠AFB=∠FBC,
又∠EFB=∠FBC,
∴∠AFB=∠BFM,
∠A=∠FMB=90°,BF=BF,
∴△AFB≌△MFB,
∴AF=FM,AB=BM,
∵BM=AB=BC,∠BME=∠C=90°,BE=BE
∴△BCE≌△BME,
∴EC=EM,
设DE=1,FM=a,则CE=k,
则FD=1+k-a,ME=CE=k
勾股定理得:DE2+FD2=EF2,
∴12+(1+k-a)2=(a+k)2
解得:a=
∴tan∠ABF=
=
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2+1 |
当DE=
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3+2 |
当DE=
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 4+3 |
…
可以发现当DE=
| 1 |
| n |
| 1 |
| n+(n-1) |
那么当DE=
| 1 |
| 5 |
| 1 |
| 5+(5-1) |
| 1 |
| 9 |

故答案为:
| 1 |
| 9 |
(2)
| 1 |
| 2k+1 |
作BM⊥EF于点M,连接BE.
∵AD∥BC,
∴∠AFB=∠FBC,
又∠EFB=∠FBC,
∴∠AFB=∠BFM,
∠A=∠FMB=90°,BF=BF,
∴△AFB≌△MFB,
∴AF=FM,AB=BM,
∵BM=AB=BC,∠BME=∠C=90°,BE=BE
∴△BCE≌△BME,
∴EC=EM,
设DE=1,FM=a,则CE=k,
则FD=1+k-a,ME=CE=k
勾股定理得:DE2+FD2=EF2,
∴12+(1+k-a)2=(a+k)2
解得:a=
| k+1 |
| 2k+1 |
∴tan∠ABF=
| a |
| k+1 |
| 1 |
| 2k+1 |
点评:此题主要考查学生对正方形的性质、全等三角形的判定与性质、勾股定理、锐角三角函数的定义的理解和掌握,涉及到的知识点较多,综合性较强,有一定的拔高难度,是一道难题.第(1)题的解答关键是通过观察题目给出的信息总结归纳出规律;第(2)题的解答关键是关键是作好辅助线.

练习册系列答案
相关题目
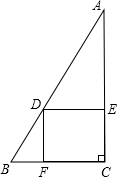 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.