摘要：25．如图14.平移抛物线F1:y＝x2后得到抛物线F2．已知抛物线F2经过抛物线F1的顶点M和点A(2.0).且对称轴与抛物线F1交于点B.设抛物线F2的顶点为N． ⑴探究四边形ABMN的形状及面积 ⑵若将已知条件中的“抛物线F1:y＝x2 改为“抛物线F1:y＝ax2 .“点A(2.0) 改为“点A(m.0) .其它条件不变.探究四边形ABMN的形状及其面积.并说明理由． ⑶若将已知条件中的“抛物线F1:y＝x2 改为“抛物线F1:y＝ax2+c. .“点A(2.0) 改为“点A(m.c) 其它条件不变.求直线AB与y轴的交点C的坐标
网址：http://m.1010jiajiao.com/timu_id_3983043[举报]
(14分)如图，抛物线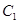
:y＝ax2＋bx+1的顶点坐标为D（1,0），
【小题1】（1）求抛物线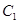的解析式；
【小题2】（2）如图1，将抛物线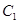向右平移1个单位，向下平移1个单位得到抛物线
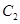，直线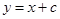
，
经过点D交y轴于点A，交抛物线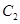于点B，抛物线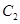的顶点为P,求△DBP的面积；
【小题3】如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上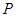点
至点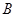
之间的一动点，
连结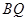
并延长交
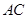于点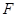
，试问：当点Q运动到什么位置时，△BCF的面积为
。
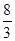查看习题详情和答案>>
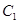:y＝ax2＋bx+1的顶点坐标为D（1,0），【小题1】（1）求抛物线
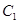的解析式；【小题2】（2）如图1，将抛物线
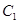向右平移1个单位，向下平移1个单位得到抛物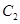线，直线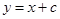，经过点D交y轴于点A，交抛物线
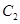于点B，抛物线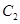的顶点为P,求△DBP的面积； 【小题3】如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
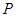至点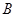之间的一动点，连结
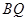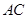并延长交于点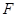，试问：当点Q运动到什么位置时，△BCF的面积为。
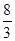查看习题详情和答案>>
(14分)如图，抛物线
:y＝ax2＋bx+1的顶点坐标为D（1,0），
1.（1）求抛物线的解析式；
2.（2）如图1，将抛物线向右平移1个单位，向下平移1个单位得到抛物线
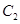，直线
，
经过点D交y轴于点A，交抛物线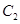于点B，抛物线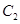的顶点为P,求△DBP的面积；
3.如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
至点
之间的一动点，
连结 
并延长交
于点
，试问：当点Q运动到什么位置时，△BCF的面积为
。
查看习题详情和答案>>
(14分)如图，抛物线
:y＝ax2＋bx+1的顶点坐标为D（1,0），
【小题1】（1）求抛物线的解析式；
【小题2】（2）如图1，将抛物线向右平移1个单位，向下平移1个单位得到抛物线
，直线
，
经过点D交y轴于点A，交抛物线于点B，抛物线的顶点为P,求△DBP的面积；
【小题3】如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
至点
之间的一动点，
连结 
并延长交
于点
，试问：当点Q运动到什么位置时，△BCF的面积为
。
:y＝ax2＋bx+1的顶点坐标为D（1,0），
，直线
，
至点
之间的一动点，
并延长交
于点
，试问：当点Q运动到什么位置时，△BCF的面积为
。