摘要： (1)证明:∵AC是圆O的直径.∴∠ABC=90 o. 又∵AD⊥BP.∴∠ADB=90 o.∴∠ABC=∠ADB. 又∵PB是圆的切线.∴∠ABD=∠ACB. 在△ABC和△ADB中: .∴△ABC∽△ADB; (2)连结OP,在Rt△AOP中.AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,又由已知可证得△ABC∽△PAO, ∴,得,解得AB=厘米.
网址：http://m.1010jiajiao.com/timu_id_3982554[举报]
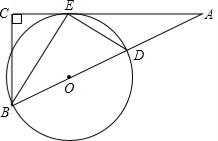（2008•雅安）如图，Rt△ABC中，∠C=90°，∠ABC的平分线交AC于E，DE⊥BE．（1）已知DE=4，BE=6，求tan∠CBE的值．
（2）证明：AC是⊙O的切线．
（2013•黔东南州）如图，在直角三角形ABC中，∠ABC=90°．（1）先作∠ACB的平分线；设它交AB边于点O，再以点O为圆心，OB为半径作⊙O（尺规作图，保留作图痕迹，不写作法）；
（2）证明：AC是所作⊙O的切线；
（3）若BC=
| 3 |
| 1 |
| 2 |
，sinA=
，求△AOC的面积．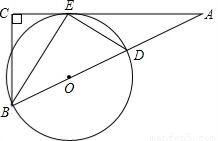
，sinA=
，求△AOC的面积．