题目内容
如图,在直角三角形ABC中,∠ABC=90°.

(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC= ,sinA=
,sinA= ,求△AOC的面积.
,求△AOC的面积.
【答案】
解:(1)作图如下::

(2)证明:过点O作OE⊥AC于点E,

∵FC平分∠ACB,
∴OB=OE。
∴AC是所作⊙O的切线。
(3)∵∠ABC=90°,sinA= ,∴∠A=30°。
,∴∠A=30°。
∴∠ACO=∠OCB= ACB=30°。
ACB=30°。
∵BC= ,∴AC=2
,∴AC=2 ,BO= BCtan30°=
,BO= BCtan30°= =1
=1
∴△AOC的面积为: ×AC×OE=
×AC×OE= ×2
×2 ×1=
×1= 。
。
【解析】
试题分析:(1)根据角平分线的作法求出角平分线FC,进而得出⊙O。
(2)根据切线的判定定理求出EO=BO,即可得出答案。
(3)根据锐角三角函数的关系求出AC,EO的长,即可得出答案。

练习册系列答案
相关题目
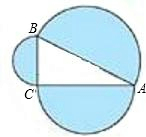 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
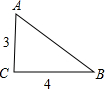
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.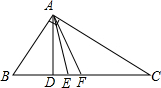 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=