摘要:已知集合U=R,UA=.B={x|x2+3(a+1)x+a2-1=0}.且A∪B=A.求实数a的取值范围. 解 ∵A={0.-6}.A∪B=A.∴BA. (1)当B=A时.由得a=1, (2)当BA时. ①若B=.则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-<a<-1. ②若B≠.则方程x2+3(a+1)x+a2-1=0有相等的实根. 即Δ=0,即a=-1或a=-.由a=-1得B={0},有BA, 由a=-,得B={}不满足BA.舍去.综上可知.-<a≤-1或a=1.
网址:http://m.1010jiajiao.com/timu_id_3981094[举报]
 UA=
UA=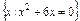 ,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围. },B={x|x2-3x+2<0},U=R,求:
},B={x|x2-3x+2<0},U=R,求: