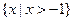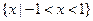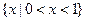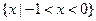题目内容
已知集合U=R, UA=
UA=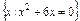 ,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
 UA=
UA=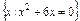 ,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.
,B={x|x2+3(a+1)x+a2-1=0},且A∪B=A,求实数a的取值范围.-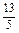 <a≤-1或a=1
<a≤-1或a=1
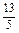 <a≤-1或a=1
<a≤-1或a=1∵A={0,-6},A∪B=A,∴B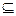 A.
A.
(1)当B=A时,由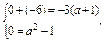 得a=1,
得a=1,
(2)当B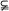 A时,
A时,
①若B=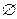 ,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-
,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-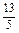 <a<-1.
<a<-1.
②若B≠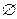 ,则方程x2+3(a+1)x+a2-1=0有相等的实根,
,则方程x2+3(a+1)x+a2-1=0有相等的实根,
即Δ=0,即a=-1或a=-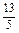 .由a=-1得B={0},有B
.由a=-1得B={0},有B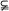 A;
A;
由a=-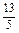 ,得B={
,得B={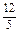 }不满足B
}不满足B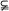 A,舍去,综上可知,-
A,舍去,综上可知,-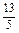 <a≤-1或a=1.
<a≤-1或a=1.
 A.
A.(1)当B=A时,由
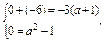 得a=1,
得a=1,(2)当B
 A时,
A时,①若B=
 ,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-
,则方程x2+3(a+1)x+a2-1=0无实根.即Δ<0,得9(a+1)2-4(a2-1)<0,解得-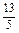 <a<-1.
<a<-1.②若B≠
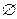 ,则方程x2+3(a+1)x+a2-1=0有相等的实根,
,则方程x2+3(a+1)x+a2-1=0有相等的实根,即Δ=0,即a=-1或a=-
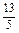 .由a=-1得B={0},有B
.由a=-1得B={0},有B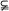 A;
A;由a=-
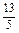 ,得B={
,得B={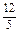 }不满足B
}不满足B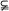 A,舍去,综上可知,-
A,舍去,综上可知,-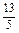 <a≤-1或a=1.
<a≤-1或a=1.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
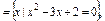 B
B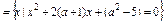
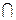 B
B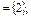 求实数a的值;
求实数a的值;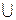 B=A求实数a的取值范围;
B=A求实数a的取值范围; UB)=A.求实数a的取值范围.
UB)=A.求实数a的取值范围.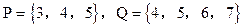 ,定义P※Q=
,定义P※Q=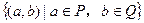 ,则
,则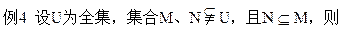 [ ]
[ ]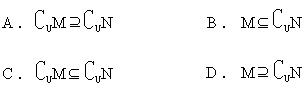
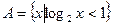 ,
,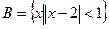 ,则集合
,则集合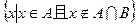 =_________。
=_________。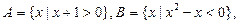 则
则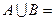 ( )
( )