摘要:设函数.证明:当.且时.. [证明]在上是减函数.在上是增函数.由且.得且.即.. [题型3] 函数的值域或最值 [例3]设a为实数.记函数的最大值为. (1)设.求t的取值范围.并把表示为t的函数, (2)求g(a), (3)试求满足的所有实数a. [解析](1)∵. ∴要使有意义.必须且.即. ∵.且--① ∴的取值范围是. 由①得:.∴.. (2)由题意知即为函数.的最大值. ∵直线是抛物线的对称轴.∴可分以下几种情况进行讨论: (1)当时.函数.的图象是开口向上的抛物线的一段. 由知在上单调递增.故, (2)当时...有=2, (3)当时..函数.的图象是开口向下的抛物线的一段. 若即时.. 若即时.. 若即时.. 综上所述.有=. (3)当时., 当时...∴. .故当时., 当时..由知:.故, 当时..故或.从而有或. 要使.必须有..即. 此时.. 综上所述.满足的所有实数a为:或. [点评]本题主要考查函数.方程等基本知识.考查分类讨论的数学思想方法和综合运用数学知识分析问题和解决问题的能力. [变式与拓展]
网址:http://m.1010jiajiao.com/timu_id_3980723[举报]
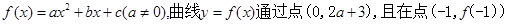
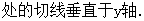
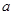 分别表示
分别表示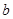 和
和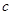 ;
;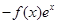 的单调区间。
的单调区间。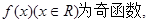
 ( )
( ) D.5
D.5