摘要： 设函数.求证:当且仅当时.在内为单调函数, [解析]. ①当时.∵.∴. ②当时.由.得, 由得, ∴当时.在上为减函数.在上为增函数. ∴当时.在 上不是单调函数. 综上.当且反当时.在上为单调函数. [题型2] 利用单调性讨论参数的范围 [例2]已知函数)的图象与函数的图象关于点对称. (1)求m的值, (2)若在区间上为减函数.求实数a的取值范围. [解析](1)设为函数图象上一点.点关于的对称点为. 则有.且. ∵点在上. ∴. 消去.代入.得. 整理.得.∴m=. (2)∵.设..且. 则对一切x1.x2∈(0.2］恒成立. ∴对一切.恒成立. ∴由.得． [变式与拓展]
网址：http://m.1010jiajiao.com/timu_id_3980722[举报]
设函数f(x)=
-ax(a＞0)，
（I）求证：当且仅当a≥1时，f（x）在[0，+∞）内为单调函数；
（II）求a的取值范围，使函数f（x）在区间[1，+∞）上是增函数．
查看习题详情和答案>>
| x2+1 |
（I）求证：当且仅当a≥1时，f（x）在[0，+∞）内为单调函数；
（II）求a的取值范围，使函数f（x）在区间[1，+∞）上是增函数．
设函数f(x)＝
－ax2，a∈R.
(1)当a＝2时，求函数f(x)的零点；
(2)当a>0时，求证：函数f(x)在(0，＋∞)内有且仅有一个零点；
(3)若函数f(x)有四个不同的零点，求a的取值范围．
设函数f(x)＝
－ax2，a∈R.
(1)当a＝2时，求函数f(x)的零点；
(2)当a>0时，求证：函数f(x)在(0，＋∞)内有且仅有一个零点；
(3)若函数f(x)有四个不同的零点，求a的取值范围．
－ax2，a∈R.(1)当a＝2时，求函数f(x)的零点；
(2)当a>0时，求证：函数f(x)在(0，＋∞)内有且仅有一个零点；
(3)若函数f(x)有四个不同的零点，求a的取值范围．
，
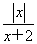
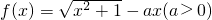