摘要:函数的最值:函数的最值是是函数值域中的特殊值.故求函数最值的方法与求值域的方法差不多.要考虑取“= 的条件是否满足. 典例剖析 [题型1]函数单调性的判断与证明 [例1]定义在上的函数..当时..且对任意的..有. (1)求证:, (2)求证:对任意的.恒有, (3)求证:是上的增函数, (4)若.求x的取值范围. [解析](1)证明:令.则.又.∴. (2)证明:当时..∴. ∴f(-x)=.又时.. ∴时.恒有. (3)证明:设.则. ∴. ∵.∴. 又.∴. ∴.∴是上的增函数. (4)解:由..得.又是上的增函数.∴.∴. [点评]解本题的关键是灵活应用题目条件.尤其是(3)中“ 是证明单调性的关键.这里体现了向条件化归的策略. [变式与拓展]
网址:http://m.1010jiajiao.com/timu_id_3980721[举报]
已知:函数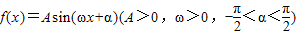 的最小正周期是π,且当
的最小正周期是π,且当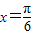 时f(x)取得最大值3.
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若x∈[0,2π),且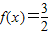 ,求x.
,求x.
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看习题详情和答案>>
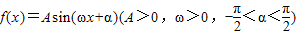 的最小正周期是π,且当
的最小正周期是π,且当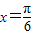 时f(x)取得最大值3.
时f(x)取得最大值3.(1)求f(x)的解析式及单调增区间.
(2)若x∈[0,2π),且
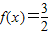 ,求x.
,求x.(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看习题详情和答案>>
已知:函数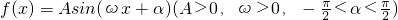 的最小正周期是π,且当
的最小正周期是π,且当 时f(x)取得最大值3.
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若x0∈[0,2π),且 ,求x0.
,求x0.
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看习题详情和答案>>
已知:函数![]() 的最小正周期是π,且当
的最小正周期是π,且当![]() 时f(x)取得最大值3.
时f(x)取得最大值3.
(1)求f(x)的解析式及单调增区间.
(2)若![]() 且
且![]() 求x0
求x0
(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
 9、图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
9、图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: