题目内容
已知:函数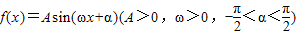 的最小正周期是π,且当
的最小正周期是π,且当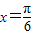 时f(x)取得最大值3.
时f(x)取得最大值3.(1)求f(x)的解析式及单调增区间.
(2)若x∈[0,2π),且
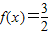 ,求x.
,求x.(3)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
【答案】分析:(1)利用函数的周期,最值,求出A,T然后求出ω,通过当 时f(x)取得最大值3求出α,从而求f(x)的解析式及单调增区间.
时f(x)取得最大值3求出α,从而求f(x)的解析式及单调增区间.
(2)若x∈[0,2π),且 ,求出x即可.
,求出x即可.
(3)利用函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求出g(x),然后再求m的最小值.
解答:解:(1)由已知条件知道: (1分)
(1分)
∴ω=2(2分)∴
∴
 ∴
∴ (3分)
(3分)
∴ (4分)
(4分)
由 可得
可得
∴f(x)的单调增区间是 (6分)
(6分)
(2) ,
,
∴ 或
或
∴x=kπ或 (9分)
(9分)
又x∈[0,2π)∴ 或
或 (11分)
(11分)
(3)由条件可得: (13分)
(13分)
又g(x)是偶函数,所以g(x)的图象关于y轴对称,
∴x=0时,g(x)取最大或最小值(14分)
即 ,
,
∴
 (15分)
(15分)
又m>0∴m的最小值是 (16分)
(16分)
点评:本题考查三角函数的最值,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换,化为一个角的一个三角函数的形式是求最值的常用方法.能够正确取得函数在给定区间上的最值,是顺利解题的前提.
 时f(x)取得最大值3求出α,从而求f(x)的解析式及单调增区间.
时f(x)取得最大值3求出α,从而求f(x)的解析式及单调增区间.(2)若x∈[0,2π),且
 ,求出x即可.
,求出x即可.(3)利用函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求出g(x),然后再求m的最小值.
解答:解:(1)由已知条件知道:
 (1分)
(1分)∴ω=2(2分)∴

∴

 ∴
∴ (3分)
(3分)∴
 (4分)
(4分)由
 可得
可得
∴f(x)的单调增区间是
 (6分)
(6分)(2)
 ,
,
∴
 或
或
∴x=kπ或
 (9分)
(9分)又x∈[0,2π)∴
 或
或 (11分)
(11分)(3)由条件可得:
 (13分)
(13分)又g(x)是偶函数,所以g(x)的图象关于y轴对称,
∴x=0时,g(x)取最大或最小值(14分)
即
 ,
,∴

 (15分)
(15分)又m>0∴m的最小值是
 (16分)
(16分)点评:本题考查三角函数的最值,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换,化为一个角的一个三角函数的形式是求最值的常用方法.能够正确取得函数在给定区间上的最值,是顺利解题的前提.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知函数y=2sin(ωx+φ)的最小正周是
,直线x=
是该函数图象的一条对称轴,则函数的解析式可以是( )
| π |
| 2 |
| π |
| 6 |
A、y=2sin(4x+
| ||
B、y=2sin(4x-
| ||
C、y=2sin(2x+
| ||
D、y=2sin(2x-
|
 ,直线x=
,直线x= 是该函数图象的一条对称轴,则函数的解析式可以是
是该函数图象的一条对称轴,则函数的解析式可以是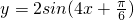
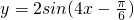
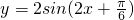
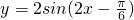
 (其中
(其中 ,
, ,
, )的最大值为2,最小正周
)的最大值为2,最小正周 .
. 的解析式;
的解析式; 的横坐标依次为
的横坐标依次为 ,
, 为坐标原点,求△
为坐标原点,求△ 的
的
 ,函数
,函数 —且最小正周斯为
—且最小正周斯为 ,
, 的最犬值,并写出相应的x的取值集合;
的最犬值,并写出相应的x的取值集合; 中角A,B,C所对的边分别为a,b,c且
中角A,B,C所对的边分别为a,b,c且 ,求b的值.
,求b的值.