摘要：设函数f(x)=x3+ax2+bx在点x=1处有极值-2. (1)求常数a,b的值, 与x轴所围成的图形的面积. 解 =3x2+2ax+b, f=0, 即.解得a=0,b=-3, 即f(x)=x3-3x. (2)作出曲线y=x3-3x的草图.所求面积为阴影部分的面积.由x3-3x=0得曲线y=x3-3x与x轴的交点坐标是(-,0),(0,0)和(,0).而y=x3-3x是R上的奇函数.函数图象关于原点中心对称. 所以(-,0)的阴影面积与(0, )的阴影面积相等. 所以所求图形的面积为 S=2［0-(x3-3x)］dx =-2(x4-x2)|=.
网址：http://m.1010jiajiao.com/timu_id_3976829[举报]
已知函数f(x)=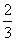
x3+ax2+bx+c．
x3+ax2+bx+c．(Ⅰ)若函数f(x)在x=1时有极值且在函数图像上的点(0，1)处的切线与直线3x+y=0平行，求f(x)的解析式；
(Ⅱ)当f(x)在x∈(0，1)取得极大值且在x∈(1，2)取得极小值时，设点M(b-2，a+1)所在平面区域为S，经过原点的直线L将S分为面积比为1：3的两部分，求直线L的方程．
查看习题详情和答案>>
x3＋ax2＋bx＋c
x3+ax2+bx+c（a＜0）在x=0处取得极值-1．