Question

已知函数f(x)=x³+ax²+bx+c．

(Ⅰ)若函数f(x)在x=1时有极值且在函数图像上的点(0，1)处的切线与直线3x+y=0平行，求f(x)的解析式；

(Ⅱ)当f(x)在x∈(0，1)取得极大值且在x∈(1，2)取得极小值时，设点M(b-2，a+1)所在平面区域为S，经过原点的直线L将S分为面积比为1：3的两部分，求直线L的方程．

Answer 1

解：(Ⅰ)由f′(x)=2x²+2ax+b，函数f(x)在x=1时有极值，

∴2a+b+2=0    ∵f(0)=1    ∴c=1

又∵f(x)在(0，1)处的切线与直线3x+y=0平行,

∴f′(0)=b=-3  故a=

∴f(x)=x³+x²-3x+1

(Ⅱ)解法一：由f′(x)=2x²+2ax+b及f(x)在x∈(0，1)取得极大值且在x∈(1，2)取得极小值，

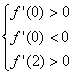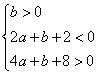∴即令M(x,y),则

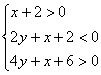∴ ∴故点M所在平面区域S为如

图△ABC，易得A(-2，0)，B(-2，-1)，C(2，-2)，D(0，-1)，E(0，)，S_△ABC=2

同时DE为△ABC的中位线，S_△DEC=S_{四边形ABED}

∴所求一条直线L的方程为：x=0

另一种情况设不垂直于x轴的直线L也将S分为面积比为1：3的两部分，设直线L方程为y=kx，它与AC、BC分别交于F、G，

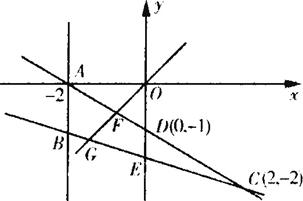
则k＞0,S_{四边形DEGF}=1

由得点F的横坐标为：x_F=

由得点G的横坐标为：x_G=

∴S_{四边形DEGF}=S_△OGE-S_△OFD.

=

即16k²+2k-5=0  解得：k=或k=(舍去)

故这时直线方程为：y=x

综上，所求直线方程为：x=0或y=x．

解法二：由f′(x)=2x²+2ax+b及f(x)在x∈(0，1)取得极大值且在x∈(1，2)取得极小值，

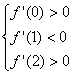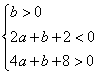∴即  令M(x,y),则

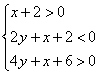∴   ∴故点M所在平面区域S为如图△ABC，易得A(-2，0)，B(-2，-1)，C(2，-2)，D(0，-1)，E(0，)，S_△ABC=2

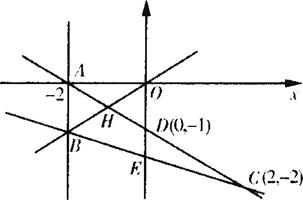
同时DE为△ABC的中位线，S_△DEC=S_{四边形ABED}

∴所求一条直线L的方程为：x=0

另一种情况由于直线BD方程为：y=x，设直线BO与AC交于H，

由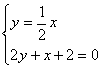得直线L与AC交点为：H(-1，)

∵S_△ABC=2，S_△DEC=×2=，

S_△ABH=S_△ABO-S_△AOH=×2×1-×2×=

∴所求直线方程为：x=0或y=x